What Is The Gcf Of 120 And 72
Arias News
May 12, 2025 · 6 min read
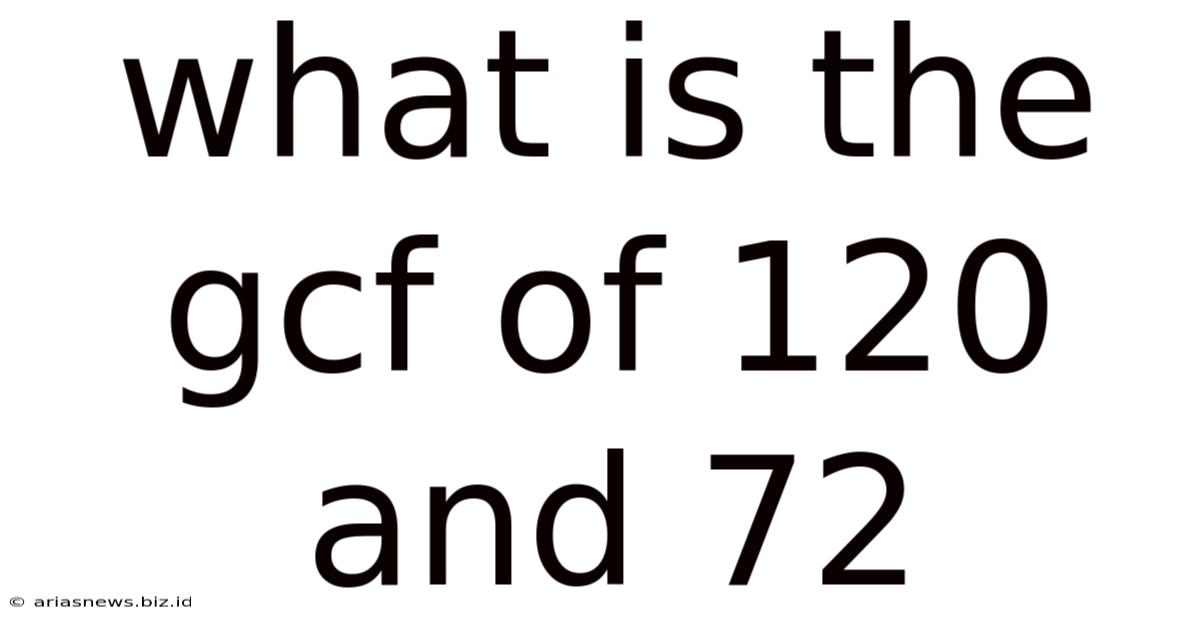
Table of Contents
What is the GCF of 120 and 72? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for solving it opens up a world of mathematical possibilities. This comprehensive guide explores the GCF of 120 and 72, explaining multiple approaches, delving into the significance of GCFs, and demonstrating their practical applications. We'll also touch upon related concepts like least common multiple (LCM) and their interconnectedness.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. Think of it as the biggest number that is a factor of both numbers. In simpler terms, it's the largest number that can be found in both numbers' multiplication tables.
For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, hence the GCF of 12 and 18 is 6.
Methods for Finding the GCF of 120 and 72
Several methods can be used to determine the GCF of 120 and 72. Let's explore some of the most common and effective approaches:
1. Listing Factors Method
This method involves listing all the factors of each number and identifying the largest common factor.
Factors of 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Comparing the lists, we can see the common factors are 1, 2, 3, 4, 6, 8, 12, and 24. The greatest of these common factors is 24. Therefore, the GCF of 120 and 72 is 24.
This method is straightforward for smaller numbers but becomes cumbersome and time-consuming for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime factorization of 120: 2³ × 3 × 5
Prime factorization of 72: 2³ × 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2³ (8) and the lowest power of 3 is 3¹ (3). Multiplying these together: 2³ × 3¹ = 8 × 3 = 24. Therefore, the GCF of 120 and 72 is 24.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are the same.
Let's apply the Euclidean algorithm to 120 and 72:
- 120 ÷ 72 = 1 with a remainder of 48
- 72 ÷ 48 = 1 with a remainder of 24
- 48 ÷ 24 = 2 with a remainder of 0
The last non-zero remainder is 24, which is the GCF of 120 and 72. This method is significantly more efficient than the previous two for larger numbers.
Significance of the GCF
Understanding the GCF is crucial in various mathematical contexts and real-world applications:
-
Simplification of Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 72/120 can be simplified by dividing both the numerator and denominator by their GCF, 24, resulting in the simplified fraction 3/5.
-
Solving Word Problems: Many word problems involving division and sharing require finding the GCF to determine the largest possible equal groups or shares. Imagine dividing 120 apples and 72 oranges into identical baskets with the maximum number of fruits per basket. The GCF (24) represents the maximum number of fruit baskets possible, with each basket containing 5 apples and 3 oranges.
-
Algebra and Number Theory: The GCF plays a fundamental role in algebra and number theory, including concepts like modular arithmetic and solving Diophantine equations.
-
Geometry and Measurement: The GCF is used in geometry to find the dimensions of the largest square tile that can be used to cover a rectangular area without any gaps or overlaps.
The Relationship Between GCF and LCM
The greatest common factor (GCF) and the least common multiple (LCM) are closely related concepts. The LCM is the smallest number that is a multiple of two or more numbers.
For two numbers, a and b, the product of their GCF and LCM is always equal to the product of the two numbers:
GCF(a, b) × LCM(a, b) = a × b
Knowing this relationship allows us to calculate the LCM if we already know the GCF (or vice-versa). Since the GCF of 120 and 72 is 24, we can calculate the LCM as follows:
LCM(120, 72) = (120 × 72) / GCF(120, 72) = (120 × 72) / 24 = 360
Therefore, the least common multiple of 120 and 72 is 360.
Real-World Applications of GCF and LCM
The GCF and LCM have numerous practical applications beyond simple mathematical exercises:
-
Scheduling: Imagine two events happening at different intervals. The LCM can help determine when both events will coincide. For instance, if event A happens every 72 days and event B happens every 120 days, they will coincide again after the LCM(72, 120) = 360 days.
-
Construction and Design: In construction, finding the GCF can help determine the size of the largest square tiles that can perfectly cover a rectangular floor without any cuts or gaps.
-
Music: In music theory, the LCM is used to determine the least common denominator when dealing with different musical rhythms.
Conclusion
Finding the greatest common factor of 120 and 72, as demonstrated using multiple methods, is more than just a simple arithmetic operation. Understanding the GCF and related concepts such as the LCM provides a deeper appreciation of number theory and its practical applications in various fields. Whether using the listing factors method, the prime factorization method, or the efficient Euclidean algorithm, the ability to calculate the GCF empowers you to solve problems efficiently and effectively, from simplifying fractions to solving complex real-world scenarios. Remember, mastering these fundamental concepts opens doors to a more comprehensive understanding of mathematics and its multifaceted applications in everyday life.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 120 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.