What Is The Gcf Of 21 And 35
Arias News
Mar 29, 2025 · 5 min read
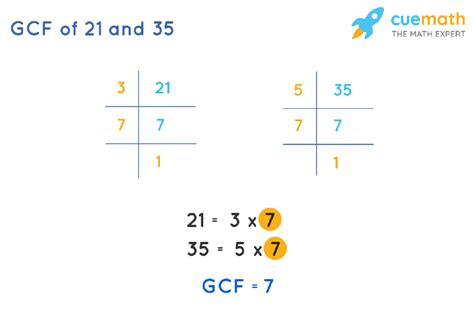
Table of Contents
What is the GCF of 21 and 35? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts and different methods for solving it opens up a world of mathematical understanding. This comprehensive guide will explore what the GCF of 21 and 35 is, and delve much deeper into the process, offering multiple approaches and highlighting the significance of GCFs in various mathematical applications.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can be divided evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without any remainder.
Finding the GCF is a fundamental concept in number theory with applications in various fields, including algebra, cryptography, and computer science. It forms the basis for simplifying fractions, solving equations, and understanding the relationships between numbers.
Methods for Finding the GCF of 21 and 35
Several methods can be used to determine the GCF of 21 and 35. Let's explore some of the most common and effective techniques:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 21: 1, 3, 7, 21
- Factors of 35: 1, 5, 7, 35
By comparing the lists, we can see that the common factors are 1 and 7. The greatest common factor is therefore 7.
2. Prime Factorization Method
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 21: 3 x 7
- Prime factorization of 35: 5 x 7
The only common prime factor is 7. Therefore, the GCF of 21 and 35 is 7.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 21 and 35:
- Start with the larger number (35) and the smaller number (21).
- Subtract the smaller number from the larger number: 35 - 21 = 14
- Now we have the numbers 21 and 14. Repeat the process. 21 - 14 = 7
- Now we have 14 and 7. Repeat the process. 14 - 7 = 7
- We now have 7 and 7. The numbers are equal, so the GCF is 7.
Therefore, the GCF of 21 and 35 using the Euclidean algorithm is 7.
Significance of GCF in Mathematics and Beyond
The concept of the greatest common factor extends far beyond simple arithmetic exercises. It plays a crucial role in various mathematical areas and practical applications:
1. Simplifying Fractions
GCF is fundamental to simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, if we want to simplify the fraction 21/35, we divide both 21 and 35 by their GCF, which is 7. This simplifies the fraction to 3/5.
2. Solving Linear Diophantine Equations
Linear Diophantine equations are equations of the form ax + by = c, where a, b, and c are integers, and we are looking for integer solutions for x and y. The existence of integer solutions depends on the GCF of a and b. If c is divisible by the GCF of a and b, then integer solutions exist. The GCF plays a vital role in finding these solutions.
3. Cryptography
GCF, particularly the Euclidean algorithm for finding it, is a cornerstone of modern cryptography. Algorithms like RSA encryption rely heavily on the properties of GCF and prime factorization to ensure secure data transmission and storage.
4. Computer Science
The GCF is used in computer science for various tasks, including:
- Data compression: Algorithms for data compression often utilize GCF to reduce the size of data files.
- Image processing: GCF is used in some image processing techniques for image scaling and manipulation.
- Scheduling algorithms: In operating systems, GCF can be used to optimize task scheduling and resource allocation.
Exploring Further: GCF and LCM
The greatest common factor (GCF) is closely related to the least common multiple (LCM). The LCM of two or more numbers is the smallest positive integer that is divisible by all the numbers. There's an interesting relationship between GCF and LCM:
For any two positive integers 'a' and 'b', the product of their GCF and LCM is equal to the product of the two numbers. Mathematically:
GCF(a, b) x LCM(a, b) = a x b
Using this relationship, if we know the GCF of two numbers, we can easily calculate their LCM, and vice-versa. For 21 and 35, we know the GCF is 7. Therefore:
7 x LCM(21, 35) = 21 x 35
LCM(21, 35) = (21 x 35) / 7 = 105
Conclusion: Mastering the GCF
Finding the greatest common factor of 21 and 35, which is 7, might seem like a simple calculation. However, understanding the various methods – listing factors, prime factorization, and the Euclidean algorithm – provides a solid foundation in number theory. Moreover, the significance of GCF extends far beyond basic arithmetic, playing a vital role in advanced mathematical concepts and practical applications in cryptography, computer science, and other fields. By mastering the concept of GCF, you unlock a deeper understanding of number relationships and their applications in various areas. The seemingly simple problem of finding the GCF of 21 and 35 is, in fact, a gateway to a vast and fascinating world of mathematical exploration.
Latest Posts
Latest Posts
-
How To Lose A Guy In Ten Days Dog
Apr 01, 2025
-
Earth Has No Sorrow That Heaven Cannot Heal Bible Verse
Apr 01, 2025
-
How Many Sig Figs Does 0 0006 Have
Apr 01, 2025
-
What Is The Square Footage Of A Football Field
Apr 01, 2025
-
How Many Days Ago Was Jesus Born
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 21 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
