What Is The Gcf Of 21 And 49
Arias News
May 11, 2025 · 5 min read
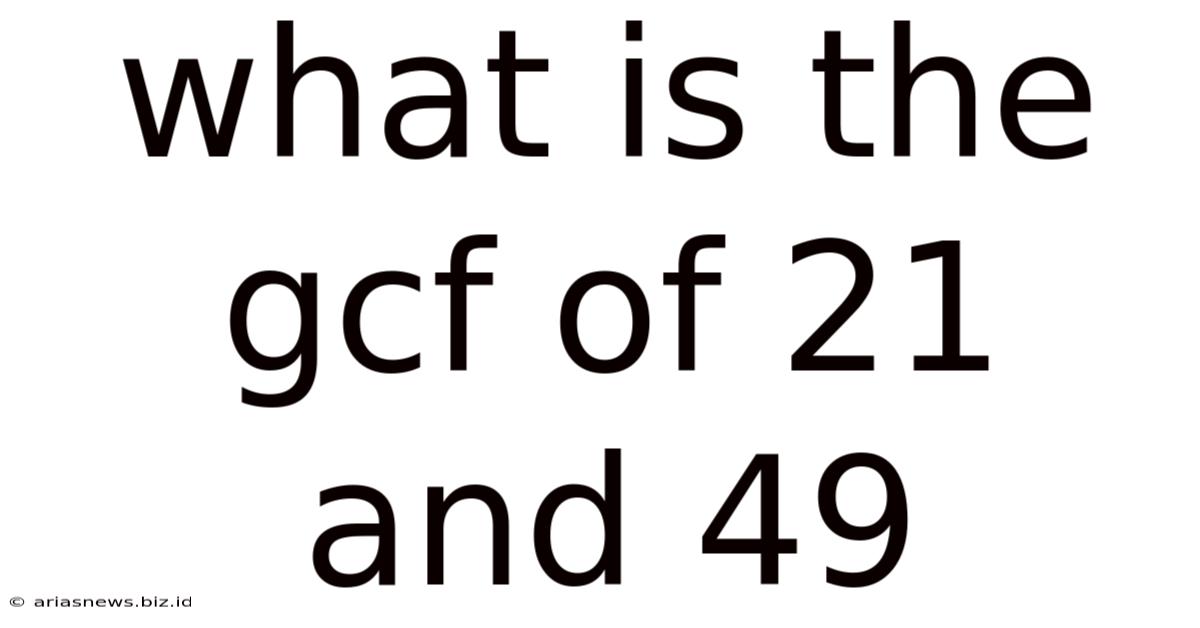
Table of Contents
What is the GCF of 21 and 49? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculation opens up a world of mathematical possibilities. This article will explore the GCF of 21 and 49 in detail, providing multiple approaches to solving the problem and delving into the broader applications of GCFs in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's a fundamental concept in number theory with significant implications in various fields like algebra, cryptography, and computer science.
Think of it like finding the largest building block that perfectly fits into two larger structures. If you have two structures made of blocks of different sizes, the GCF represents the size of the largest block that can be used to build both structures.
In the case of 21 and 49, we're looking for the biggest number that divides both 21 and 49 without leaving a remainder.
Method 1: Prime Factorization
The most common and often the most efficient method to find the GCF is through prime factorization. This involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Let's prime factorize 21 and 49:
- 21: The prime factorization of 21 is 3 x 7.
- 49: The prime factorization of 49 is 7 x 7.
Now, we identify the common prime factors. Both 21 and 49 share one prime factor: 7. We then multiply these common prime factors together to find the GCF.
Therefore, the GCF of 21 and 49 is 7.
Method 2: Listing Factors
Another approach, albeit less efficient for larger numbers, involves listing all the factors of each number and identifying the largest common factor.
Factors of 21: 1, 3, 7, 21 Factors of 49: 1, 7, 49
Comparing the lists, we see that the common factors are 1 and 7. The largest of these common factors is 7. Therefore, the GCF of 21 and 49 is 7.
This method becomes cumbersome when dealing with larger numbers, highlighting the advantage of prime factorization for efficiency.
Method 3: Euclidean Algorithm
For larger numbers, the Euclidean algorithm provides a more efficient method than listing factors. This iterative algorithm uses the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal. That equal number is the GCF.
Let's apply the Euclidean algorithm to 21 and 49:
- 49 - 21 = 28 (Now we find the GCF of 21 and 28)
- 28 - 21 = 7 (Now we find the GCF of 7 and 21)
- Since 21 is a multiple of 7 (21 = 7 x 3), the GCF is 7.
Therefore, the GCF of 21 and 49 is 7.
The Euclidean algorithm is particularly useful for larger numbers where prime factorization can become computationally intensive.
Applications of GCF in Real-World Scenarios
The concept of GCF extends beyond abstract mathematical problems and finds practical applications in various fields:
-
Simplifying Fractions: The GCF plays a crucial role in simplifying fractions to their lowest terms. By dividing both the numerator and denominator by their GCF, we obtain an equivalent fraction in its simplest form. For example, the fraction 21/49 can be simplified to 3/7 by dividing both the numerator and denominator by their GCF, which is 7.
-
Dividing Objects Equally: Consider scenarios where you need to divide a collection of items into equal groups. The GCF helps determine the largest possible group size. For instance, if you have 21 apples and 49 oranges, and you want to create groups with the same number of apples and oranges in each group, the largest group size you can have is 7.
-
Geometry and Measurement: GCF is frequently used in geometric problems, such as finding the side length of the largest square that can be used to tile a rectangular area. If the dimensions of the rectangle are 21 units and 49 units, the largest square you can tile would have sides of length 7 units.
-
Computer Science and Cryptography: The GCF is fundamental in many computer algorithms, including those used in cryptography for tasks such as key generation and encryption. Efficient GCF calculations are essential for the security and performance of these systems.
Expanding the Concept: GCF of More Than Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. Using prime factorization, we simply find the common prime factors across all the numbers and multiply them together. For the Euclidean algorithm, we can iteratively find the GCF of pairs of numbers, reducing the problem step-by-step.
For instance, to find the GCF of 21, 49, and 63:
-
Prime Factorization:
- 21 = 3 x 7
- 49 = 7 x 7
- 63 = 3 x 3 x 7
The only common prime factor is 7. Therefore, the GCF(21, 49, 63) = 7
-
Euclidean Algorithm (Iterative):
- First, find the GCF(21, 49) = 7 (as shown previously)
- Then, find the GCF(7, 63) = 7.
Therefore, the GCF(21, 49, 63) = 7
Conclusion: Mastering the GCF
Understanding the greatest common factor is essential for a strong foundation in mathematics and its practical applications. Whether you use prime factorization, listing factors, or the Euclidean algorithm, the choice of method depends on the complexity of the numbers involved. This article has explored multiple approaches to calculating the GCF of 21 and 49, demonstrating the versatility and importance of this fundamental concept in various fields. Remember, mastering the GCF not only enhances your mathematical skills but also equips you with a valuable tool for problem-solving in diverse real-world situations.
Latest Posts
Latest Posts
-
How Many Pints Are In A Pound Of Sour Cream
May 12, 2025
-
Did Jim Nabors Sing At The Kentucky Derby
May 12, 2025
-
How Much Does A Concrete Block Weight 8x8x16
May 12, 2025
-
Greatest Common Factor Of 8 And 36
May 12, 2025
-
4 Out Of 20 As A Grade
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 21 And 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.