What Is The Gcf Of 27 And 18
Arias News
May 11, 2025 · 5 min read
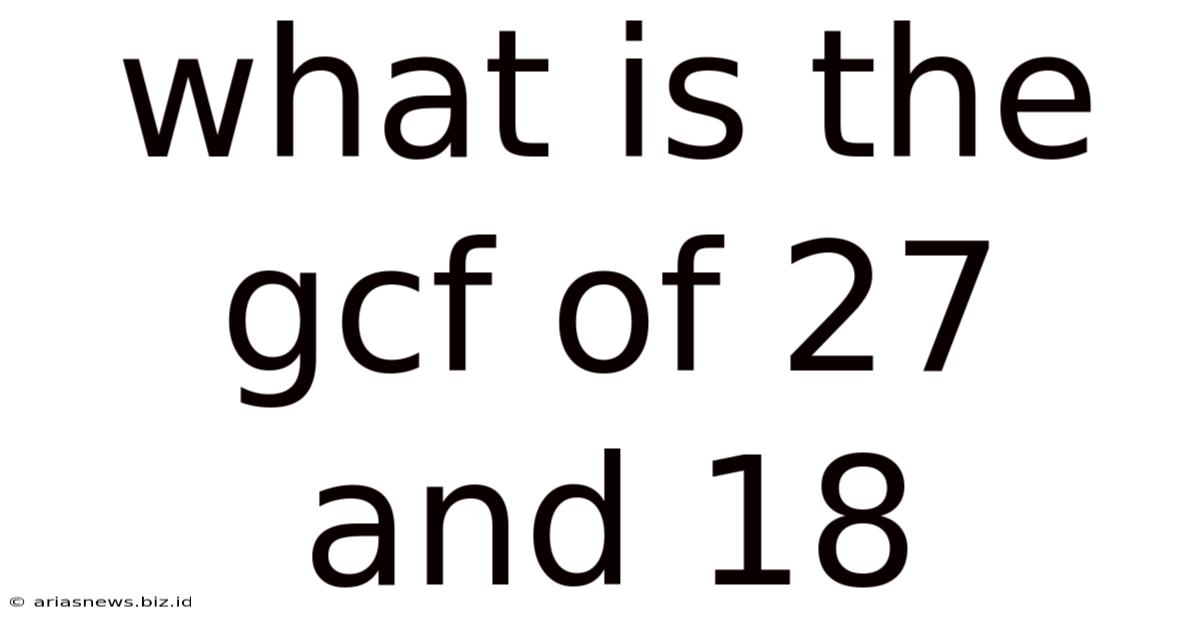
Table of Contents
What is the GCF of 27 and 18? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for solving it opens doors to more advanced mathematical concepts. This comprehensive guide will not only answer the question, "What is the GCF of 27 and 18?" but will also explore various techniques to determine the GCF of any two numbers, highlighting their applications in various fields.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. It's a fundamental concept in number theory with applications in algebra, geometry, and cryptography. Essentially, it's the biggest number that perfectly divides both numbers.
For example, let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 18 is 6.
Methods for Finding the GCF
Several methods exist for finding the GCF, each with its own strengths and weaknesses. Let's explore the most common ones:
1. Listing Factors
This is the most straightforward method, especially for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Example: Finding the GCF of 27 and 18
- Factors of 27: 1, 3, 9, 27
- Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1, 3, and 9. Therefore, the GCF of 27 and 18 is 9.
This method becomes cumbersome for larger numbers, making it less efficient.
2. Prime Factorization
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Steps:
- Find the prime factorization of each number: Break down each number into its prime factors.
- Identify common prime factors: Find the prime factors that appear in both factorizations.
- Multiply the common prime factors: Multiply the common prime factors together to get the GCF.
Example: Finding the GCF of 27 and 18 using prime factorization
- Prime factorization of 27: 3 x 3 x 3 = 3³
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
The common prime factor is 3, appearing twice in both factorizations (3²). Therefore, the GCF of 27 and 18 is 3 x 3 = 9.
This method is more efficient than listing factors, especially for larger numbers, as it avoids the need to list all factors.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
- Divide the larger number by the smaller number: Find the quotient and remainder.
- Replace the larger number with the smaller number: The smaller number becomes the new larger number.
- Replace the smaller number with the remainder: The remainder becomes the new smaller number.
- Repeat steps 1-3: Continue this process until the remainder is 0.
- The GCF is the last non-zero remainder: The last non-zero remainder is the GCF of the original two numbers.
Example: Finding the GCF of 27 and 18 using the Euclidean Algorithm
- 27 ÷ 18 = 1 with a remainder of 9
- 18 ÷ 9 = 2 with a remainder of 0
The last non-zero remainder is 9. Therefore, the GCF of 27 and 18 is 9.
Applications of the GCF
The GCF has numerous applications across various fields:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. Dividing both the numerator and denominator by their GCF results in an equivalent fraction in its simplest form. For example, the fraction 27/18 simplifies to 3/2 by dividing both numerator and denominator by their GCF, which is 9.
-
Solving Word Problems: Many real-world problems involving equal groupings or divisions require finding the GCF. For instance, imagine you have 27 apples and 18 oranges and you want to divide them into identical bags with the largest possible number of fruits in each bag. The GCF of 27 and 18 (which is 9) determines the maximum number of fruits per bag.
-
Geometry: The GCF is used in geometry to determine the dimensions of the largest square that can be used to tile a rectangle. If you have a rectangle with dimensions 27 units by 18 units, the largest square that can tile this rectangle has a side length equal to the GCF of 27 and 18 (which is 9 units).
-
Cryptography: The GCF plays a significant role in cryptography, particularly in RSA encryption, which relies heavily on prime factorization and the GCF for its security.
Beyond Two Numbers: Finding the GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors with the lowest exponent. For the Euclidean Algorithm, you would find the GCF of two numbers, and then find the GCF of the result and the next number, and so on.
Conclusion: Mastering the GCF
Understanding how to find the greatest common factor is a valuable skill with far-reaching implications. Whether you’re simplifying fractions, solving geometric problems, or exploring the intricacies of number theory, mastering the GCF equips you with a fundamental tool for tackling various mathematical challenges. This guide has provided multiple methods, each with its own advantages, ensuring you can effectively determine the GCF regardless of the numbers involved. So, next time you encounter a problem requiring the GCF, remember the techniques discussed here and confidently find the solution!
Latest Posts
Latest Posts
-
Why Nh3 Is More Polar Than Nf3
May 12, 2025
-
Distance From Tampa To Cancun By Boat
May 12, 2025
-
Is A Mcg Smaller Than A Mg
May 12, 2025
-
How Far Am I From Wichita Kansas
May 12, 2025
-
How Many Feet Are In A Yardstick
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 27 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.