What Is The Gcf Of 36 And 42
Arias News
Mar 29, 2025 · 5 min read
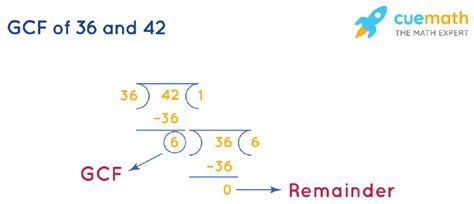
Table of Contents
What is the GCF of 36 and 42? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and various methods for calculating the GCF is crucial for a strong foundation in mathematics. This in-depth exploration will not only answer the question "What is the GCF of 36 and 42?" but also delve into the various techniques to find the GCF of any two numbers, expanding your understanding beyond this specific example. We'll explore prime factorization, the Euclidean algorithm, and the listing factors method, providing you with a versatile toolkit for tackling GCF problems.
Understanding Greatest Common Factor (GCF)
Before we jump into calculating the GCF of 36 and 42, let's define what the GCF actually is. The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers.
Think of it like finding the largest shared building block of two numbers. Just like you can build with LEGO bricks of different sizes, numbers can be built from smaller prime number "bricks." The GCF represents the largest set of these shared "bricks."
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Then, we identify the common prime factors and multiply them together to find the GCF.
Let's apply this to 36 and 42:
1. Prime Factorization of 36:
36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3²
2. Prime Factorization of 42:
42 = 2 x 21 = 2 x 3 x 7
3. Identifying Common Prime Factors:
Both 36 and 42 share one factor of 2 and one factor of 3.
4. Calculating the GCF:
GCF(36, 42) = 2 x 3 = 6
Therefore, the greatest common factor of 36 and 42 is 6.
Advantages and Disadvantages of Prime Factorization:
Advantages:
- Provides a clear understanding of the number's composition.
- Works well for smaller numbers.
Disadvantages:
- Can become cumbersome with very large numbers.
- Requires knowledge of prime numbers and their identification.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply this to 36 and 42:
1. Start with the larger number (42) and the smaller number (36):
42 = 1 x 36 + 6
2. Replace the larger number (42) with the remainder (6) and repeat:
36 = 6 x 6 + 0
3. The process stops when the remainder is 0. The GCF is the last non-zero remainder:
The last non-zero remainder is 6.
Therefore, the GCF(36, 42) = 6.
Advantages and Disadvantages of the Euclidean Algorithm:
Advantages:
- Efficient for large numbers.
- Doesn't require prime factorization.
- Systematic and easy to follow.
Disadvantages:
- May not be as intuitive as prime factorization for beginners.
Method 3: Listing Factors
This is a more straightforward method, suitable for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
1. List Factors of 36:
1, 2, 3, 4, 6, 9, 12, 18, 36
2. List Factors of 42:
1, 2, 3, 6, 7, 14, 21, 42
3. Identify Common Factors:
The common factors of 36 and 42 are 1, 2, 3, and 6.
4. Determine the Greatest Common Factor:
The largest common factor is 6.
Therefore, the GCF(36, 42) = 6.
Advantages and Disadvantages of Listing Factors:
Advantages:
- Simple and easy to understand.
- Works well for small numbers.
Disadvantages:
- Can become time-consuming and inefficient for larger numbers.
- Prone to errors if factors are missed.
Applications of GCF in Real-World Scenarios
Understanding the GCF is not just an academic exercise; it has practical applications in various fields:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 36/42 can be simplified to 6/7 by dividing both the numerator and denominator by their GCF (6).
-
Geometry: GCF is used in solving geometry problems involving areas and perimeters. For instance, finding the dimensions of the largest square tile that can evenly cover a rectangular floor with dimensions 36 and 42 units. The solution would be a 6 x 6 unit square.
-
Data Organization: In data analysis and organization, GCF helps in grouping data efficiently. Consider arranging 36 apples and 42 oranges into the largest possible equal groups. You could create 6 groups, each containing 6 apples and 7 oranges.
Expanding Your Understanding: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For prime factorization, you'd find the prime factorization of each number and identify the common prime factors with the lowest power. For the Euclidean algorithm, you can apply it iteratively, first finding the GCF of two numbers, then finding the GCF of the result and the next number, and so on.
Conclusion: Mastering GCF Calculations
Finding the GCF, whether it's for the seemingly simple case of 36 and 42 or for more complex scenarios, is a fundamental skill in mathematics. Mastering various methods, including prime factorization, the Euclidean algorithm, and the listing factors method, equips you with the tools to efficiently and accurately determine the GCF in diverse applications. Remember to choose the method best suited to the numbers involved – prime factorization for smaller numbers, and the Euclidean algorithm for efficiency with larger numbers. Understanding the underlying principles behind GCF calculations empowers you to solve a wide range of mathematical problems and enhances your problem-solving capabilities across various disciplines. The ability to efficiently determine the GCF lays the foundation for more advanced mathematical concepts and applications.
Latest Posts
Latest Posts
-
Only What You Do For Christ Will Last Scripture
Mar 31, 2025
-
How Many Square Miles Is 200000 Acres
Mar 31, 2025
-
How Do You Say 41 In Spanish
Mar 31, 2025
-
How Do You Give A Hand Job
Mar 31, 2025
-
How Old Are You If You Were Born In 1953
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 36 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
