What Is The Gcf Of 42 And 54
Arias News
Apr 02, 2025 · 5 min read
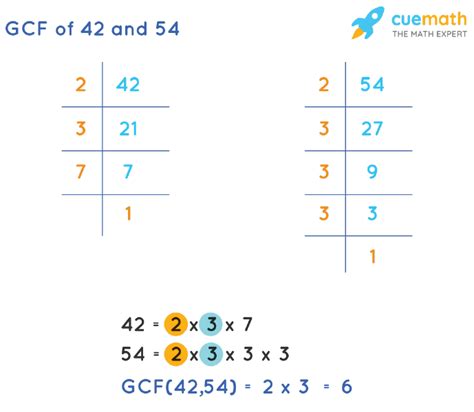
Table of Contents
What is the GCF of 42 and 54? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can unlock a deeper appreciation of number theory. This article will not only answer the question, "What is the GCF of 42 and 54?" but also delve into various approaches to finding the GCF, exploring their applications, and illustrating their importance in various mathematical contexts.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides both of two or more integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. GCFs are fundamental in simplifying fractions, solving algebraic equations, and understanding the relationships between different numbers.
Let's consider our specific problem: finding the GCF of 42 and 54. This means we're looking for the largest number that perfectly divides both 42 and 54.
Method 1: Prime Factorization
This is a classic and reliable method for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 42
42 can be factored as: 2 x 3 x 7
Step 2: Prime Factorization of 54
54 can be factored as: 2 x 3 x 3 x 3 or 2 x 3³
Step 3: Identifying Common Factors
Now, we compare the prime factorizations of 42 and 54:
42 = 2 x 3 x 7 54 = 2 x 3 x 3 x 3
Both numbers share a factor of 2 and a factor of 3.
Step 4: Calculating the GCF
The GCF is the product of the common prime factors: 2 x 3 = 6
Therefore, the GCF of 42 and 54 is 6.
Method 2: Listing Factors
This method is straightforward, especially for smaller numbers. We list all the factors of each number and then identify the largest common factor.
Step 1: Factors of 42
The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, 42
Step 2: Factors of 54
The factors of 54 are: 1, 2, 3, 6, 9, 18, 27, 54
Step 3: Identifying Common Factors
Comparing the lists, we find the common factors: 1, 2, 3, 6
Step 4: Determining the GCF
The largest common factor is 6. Therefore, the GCF of 42 and 54 is 6.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Step 1: Initial Numbers
We start with our two numbers: 42 and 54.
Step 2: Repeated Subtraction
54 - 42 = 12 (Now we find the GCF of 42 and 12) 42 - 12 = 30 (Now we find the GCF of 12 and 30) 30 - 12 = 18 (Now we find the GCF of 12 and 18) 18 - 12 = 6 (Now we find the GCF of 12 and 6) 12 - 6 = 6 (Now we find the GCF of 6 and 6)
Since both numbers are now 6, the GCF is 6.
Method 4: Euclidean Algorithm (Division Method)
This is a more efficient variation of the Euclidean algorithm. Instead of repeated subtraction, we use division with remainder.
Step 1: Division
Divide the larger number (54) by the smaller number (42):
54 ÷ 42 = 1 with a remainder of 12
Step 2: Iteration
Now, we repeat the process using the divisor (42) and the remainder (12):
42 ÷ 12 = 3 with a remainder of 6
Step 3: Final Division
Finally, we divide the previous divisor (12) by the last remainder (6):
12 ÷ 6 = 2 with a remainder of 0
Step 4: Result
When the remainder is 0, the GCF is the last non-zero remainder, which is 6.
Applications of GCF
The GCF has numerous applications across various mathematical fields and real-world scenarios:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows you to simplify fractions to their lowest terms. For example, the fraction 42/54 can be simplified to 7/9 by dividing both the numerator and denominator by their GCF, 6.
-
Solving Diophantine Equations: These equations involve finding integer solutions. The GCF plays a crucial role in determining the existence and nature of these solutions.
-
Modular Arithmetic: GCF is essential in understanding modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus).
-
Cryptography: GCF is a cornerstone of various cryptographic algorithms, which are used to secure communication and data.
-
Geometry: GCF helps in solving geometric problems involving the dimensions of shapes and their relationships. For example, finding the greatest common divisor of the lengths of two sides helps to determine common factors in area or volume calculations.
Beyond the Basics: Exploring Further Concepts
While we've focused on finding the GCF of two numbers, the concept extends to finding the GCF of three or more numbers. The same methods, particularly prime factorization and the Euclidean algorithm, can be adapted to handle multiple numbers. Simply find the GCF of the first two numbers and then find the GCF of that result and the third number, and so on.
Furthermore, the concept of the least common multiple (LCM) is closely related to the GCF. The LCM is the smallest positive integer that is a multiple of two or more integers. The GCF and LCM are linked by the following relationship:
(GCF of a and b) x (LCM of a and b) = a x b
Conclusion
Finding the GCF of 42 and 54, as demonstrated through multiple methods, highlights the versatility and importance of this fundamental concept in number theory. Whether you use prime factorization, listing factors, or the Euclidean algorithm, the result remains the same: the GCF of 42 and 54 is 6. Understanding these methods not only helps solve specific problems but also provides a deeper insight into the structure and relationships within the number system. This knowledge extends far beyond simple arithmetic, impacting diverse mathematical areas and real-world applications. The exploration of GCF, therefore, is an enriching journey into the fascinating world of numbers and their inherent properties.
Latest Posts
Latest Posts
-
How Many Minutes Are In 999 Seconds
Apr 03, 2025
-
How Many Cups Of Chicken Broth Are In A Box
Apr 03, 2025
-
Four Letter Words Starting And Ending With The Same Letter
Apr 03, 2025
-
Is Brown Hair And Blue Eyes Rare
Apr 03, 2025
-
We Will All Laugh At Gilded Butterflies Meaning
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 42 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
