What Is The Gcf Of 64 And 48
Arias News
Apr 03, 2025 · 5 min read
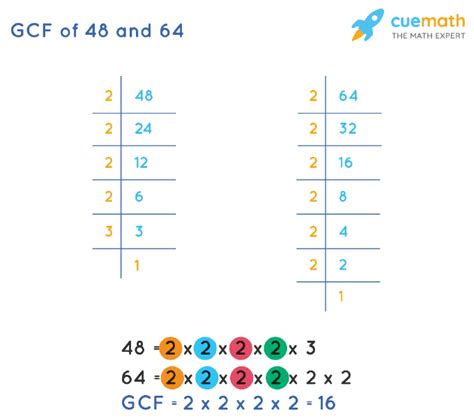
Table of Contents
What is the GCF of 64 and 48? A Deep Dive into Finding the Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring various methods can be surprisingly enriching. This comprehensive guide will not only answer the question, "What is the GCF of 64 and 48?" but will also delve into the theoretical underpinnings of GCFs, explore multiple solution methods, and demonstrate their practical applications.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. Understanding GCFs is crucial in various mathematical applications, including simplifying fractions, solving algebraic equations, and even in advanced areas like cryptography.
Why is finding the GCF important?
The importance of finding the GCF extends beyond simple arithmetic. Here are some key applications:
- Simplifying Fractions: The GCF is essential for reducing fractions to their simplest form. For example, the fraction 48/64 can be simplified using the GCF.
- Solving Algebraic Equations: GCFs play a crucial role in factoring polynomials, a fundamental technique in algebra.
- Geometry and Measurement: GCFs are used in problems involving finding the dimensions of the largest square tile that can perfectly cover a rectangular area.
- Number Theory: GCF is a foundational concept in number theory, leading to more advanced topics like modular arithmetic and cryptography.
Methods for Finding the GCF of 64 and 48
There are several effective methods for determining the greatest common factor of two numbers. Let's explore some of the most common and useful approaches.
1. Prime Factorization Method
This is a classic and highly reliable method. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Step 1: Prime Factorization of 64
64 can be factored as follows:
64 = 2 x 32 = 2 x 2 x 16 = 2 x 2 x 2 x 8 = 2 x 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 x 2 = 2<sup>6</sup>
Step 2: Prime Factorization of 48
48 can be factored as follows:
48 = 2 x 24 = 2 x 2 x 12 = 2 x 2 x 2 x 6 = 2 x 2 x 2 x 2 x 3 = 2<sup>4</sup> x 3
Step 3: Identifying Common Factors
Now, we compare the prime factorizations of 64 and 48:
64 = 2<sup>6</sup> 48 = 2<sup>4</sup> x 3
The common prime factor is 2, and the lowest power of 2 present in both factorizations is 2<sup>4</sup>.
Step 4: Calculating the GCF
Therefore, the GCF of 64 and 48 is 2<sup>4</sup> = 16.
2. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Step 1: Factors of 64
The factors of 64 are: 1, 2, 4, 8, 16, 32, 64
Step 2: Factors of 48
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Step 3: Identifying Common Factors
Comparing the lists, the common factors are 1, 2, 4, 8, and 16.
Step 4: Determining the GCF
The greatest common factor among these is 16.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for larger numbers. It's based on the principle of repeated division with remainder.
Step 1: Divide the larger number by the smaller number
64 ÷ 48 = 1 with a remainder of 16
Step 2: Replace the larger number with the smaller number, and the smaller number with the remainder
Now we consider 48 and 16.
48 ÷ 16 = 3 with a remainder of 0
Step 3: The GCF is the last non-zero remainder
Since the remainder is 0, the GCF is the last non-zero remainder, which is 16.
The GCF of 64 and 48: The Answer and its Significance
Through all three methods – prime factorization, listing factors, and the Euclidean algorithm – we consistently arrive at the same answer: The GCF of 64 and 48 is 16.
This result has practical implications. For example, if you have a rectangular area of 64 square units and another of 48 square units, the largest square tiles you could use to cover both areas without any cutting would be 16 square units in size. Similarly, the fraction 48/64 can be simplified to 3/4 by dividing both the numerator and denominator by their GCF, 16.
Expanding the Concept: GCF and LCM
The greatest common factor (GCF) is closely related to the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of both numbers. For 64 and 48, the LCM is 192. There's an important relationship between the GCF and LCM:
GCF(a, b) x LCM(a, b) = a x b
In our case:
16 x 192 = 3072 64 x 48 = 3072
This relationship provides a useful shortcut for finding the LCM if you already know the GCF (or vice-versa).
Practical Applications Beyond Basic Arithmetic
The concept of the greatest common factor extends far beyond simple number theory. Here are some real-world applications:
- Software Development: GCFs are used in algorithms for optimizing data structures and processes.
- Cryptography: The GCF plays a crucial role in public-key cryptography, underpinning many secure online transactions.
- Music Theory: GCFs help in understanding musical intervals and harmonies.
- Engineering and Design: GCFs are used in optimizing designs and resource allocation.
Conclusion: Mastering the GCF
Understanding how to find the greatest common factor is a valuable skill with applications in various fields. This article has provided a comprehensive overview of the GCF, explored different methods for calculating it, and highlighted its relevance in various contexts. Whether you're a student tackling arithmetic problems or a professional applying mathematical concepts in your work, a firm grasp of the GCF will serve you well. Remember the three methods explored – prime factorization, listing factors, and the Euclidean algorithm – and choose the one that best suits your needs and the size of the numbers involved. Mastering the GCF is not just about finding the answer; it’s about understanding the underlying principles and appreciating its far-reaching applications.
Latest Posts
Latest Posts
-
How Many Square Meters Is A Football Field
Apr 04, 2025
-
How Many Square Feet In 31 Acres
Apr 04, 2025
-
Is Freddie Jackson Related To Michael Jackson
Apr 04, 2025
-
What Is Always Included In A Comparative Investigation
Apr 04, 2025
-
Can You Buy Lottery Tickets With A Gift Card
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 64 And 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
