What Is The Gcf Of 8 And 32
Arias News
May 12, 2025 · 5 min read
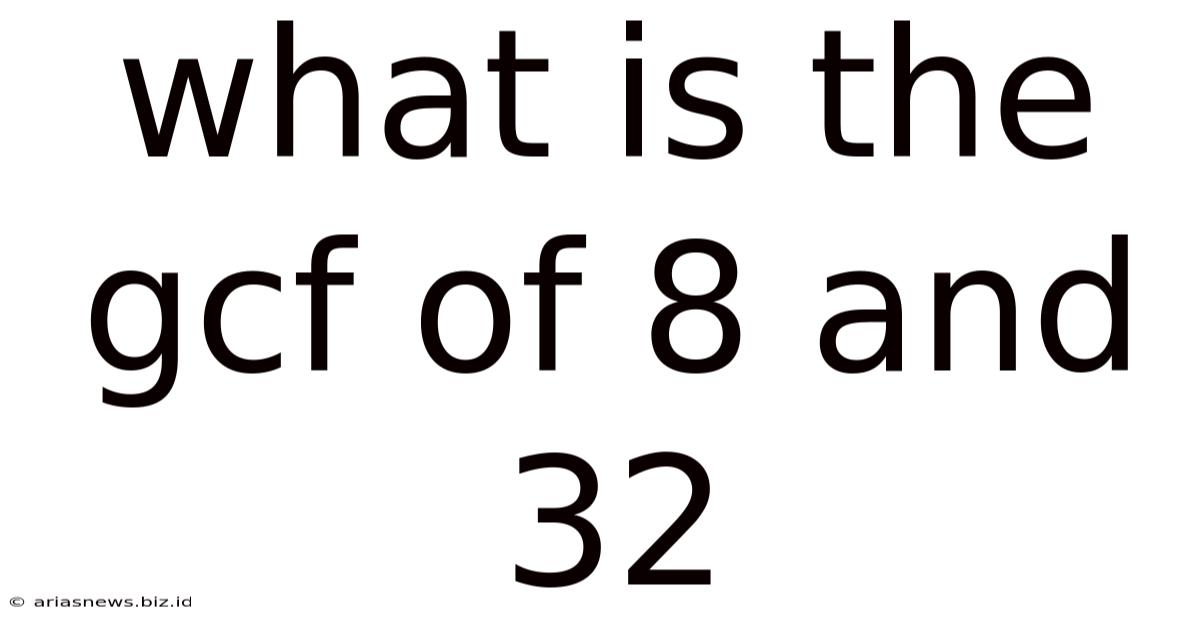
Table of Contents
What is the GCF of 8 and 32? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it is crucial for a strong foundation in mathematics. This article will not only answer the question "What is the GCF of 8 and 32?" but also explore the broader topic of GCFs, delving into multiple approaches, real-world applications, and related mathematical concepts.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. Understanding GCFs is essential in various mathematical operations, from simplifying fractions to solving algebraic equations.
For example, let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 18 is 6.
Calculating the GCF of 8 and 32
Now, let's address the central question: what is the GCF of 8 and 32? We can use several methods to find this:
Method 1: Listing Factors
The most straightforward method is listing all the factors of each number and identifying the largest common factor.
- Factors of 8: 1, 2, 4, 8
- Factors of 32: 1, 2, 4, 8, 16, 32
Comparing the two lists, we see that the common factors are 1, 2, 4, and 8. The greatest of these is 8.
Therefore, the GCF of 8 and 32 is 8.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. This method is particularly useful for larger numbers.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2⁵
To find the GCF, we identify the common prime factors and take the lowest power of each. In this case, the only common prime factor is 2, and the lowest power is 2³.
Therefore, the GCF of 8 and 32 is 2³ = 8.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 8 and 32:
- 32 ÷ 8 = 4 with a remainder of 0. Since the remainder is 0, the GCF is the smaller number, which is 8.
Therefore, the GCF of 8 and 32 is 8.
Real-World Applications of GCF
The concept of GCF has practical applications in various fields:
-
Simplifying Fractions: To simplify a fraction to its lowest terms, we divide both the numerator and the denominator by their GCF. For example, to simplify the fraction 32/8, we find the GCF of 32 and 8 (which is 8) and divide both by 8, resulting in the simplified fraction 4/1, or simply 4.
-
Dividing Objects Evenly: Imagine you have 32 apples and you want to divide them equally among 8 friends. The GCF (8) tells you that each friend will receive 4 apples.
-
Geometry: GCF is used in determining the dimensions of the largest square tile that can be used to cover a rectangular area without any gaps or overlaps. For instance, if you have a rectangular area of 32 feet by 8 feet, the GCF (8) represents the side length of the largest square tile you can use (8x8 feet tiles).
-
Music Theory: GCF is used to simplify musical ratios, often represented as fractions. Understanding the GCF between the frequencies of two notes helps determine the intervals between them.
-
Project Management: Finding the GCF can be useful when scheduling tasks that need to be completed in different time intervals. The GCF helps to find a common time period for scheduling.
Beyond the Basics: Exploring Related Concepts
Understanding GCF lays a foundation for grasping related mathematical concepts:
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is a multiple of each of the integers. GCF and LCM are related through the formula: (GCF x LCM) = (Product of the two numbers). This relationship is helpful in solving problems involving fractions and ratios.
-
Modular Arithmetic: GCF plays a vital role in modular arithmetic, which deals with remainders after division. Concepts like finding the multiplicative inverse rely heavily on the GCF.
Conclusion: Mastering GCF for Mathematical Proficiency
The seemingly simple concept of the greatest common factor unlocks a wealth of mathematical understanding. Knowing how to calculate the GCF using different methods, understanding its applications in various fields, and recognizing its connections to other mathematical concepts are key elements in developing mathematical proficiency. From simplifying fractions to tackling complex algebraic equations, the GCF provides a fundamental building block for numerous mathematical endeavors. This article has explored the calculation of the GCF of 8 and 32 in detail, demonstrating various approaches and highlighting its significance in a wide range of practical scenarios. The next time you encounter a problem involving GCF, you'll be well-equipped to tackle it with confidence.
Latest Posts
Latest Posts
-
How To Address A Letter To A Nursing Home Resident
May 12, 2025
-
Can Bearded Dragons Eat Brussel Sprout Leaves
May 12, 2025
-
How Many Right Angles Does Trapezoid Have
May 12, 2025
-
Kohler 52 50 02 S Cross Reference
May 12, 2025
-
How Much Is 1 Acre Of Land In Mexico
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 8 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.