What Is The Greatest Common Factor For 18 And 30
Arias News
May 10, 2025 · 6 min read
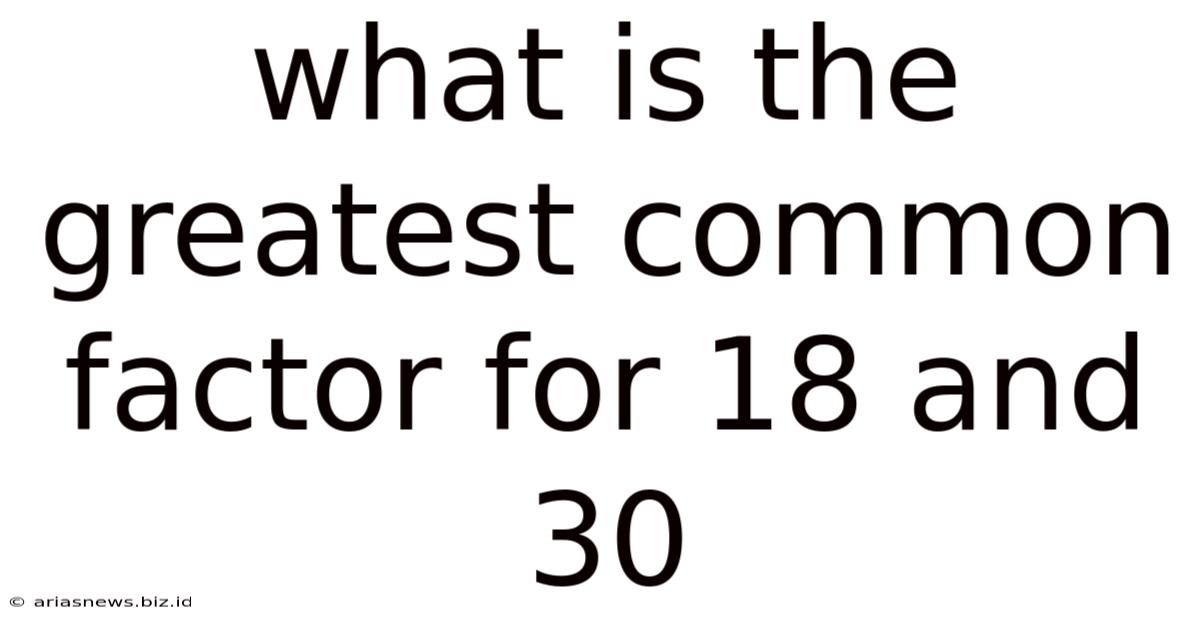
Table of Contents
What is the Greatest Common Factor for 18 and 30? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can unlock a deeper appreciation for number theory and its applications. This comprehensive guide will not only answer the question "What is the greatest common factor for 18 and 30?" but also equip you with the knowledge and skills to efficiently determine the GCF for any pair of numbers. We'll delve into various methods, explore real-world applications, and even touch upon the historical context of this fundamental concept.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. For instance, if we consider the numbers 12 and 18, the common factors are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Why is the GCF Important?
The concept of GCF is crucial in various mathematical applications, including:
- Simplifying Fractions: The GCF helps in reducing fractions to their simplest form. For example, the fraction 18/30 can be simplified by dividing both the numerator and denominator by their GCF.
- Algebraic Simplification: GCF plays a significant role in simplifying algebraic expressions by factoring out common terms.
- Solving Word Problems: Many real-world problems involving division and sharing require determining the GCF to find the optimal solution.
- Geometry and Measurement: GCF is used in determining the dimensions of objects or finding the largest possible size for tiles or blocks when covering an area.
Methods for Finding the GCF of 18 and 30
Several methods can effectively determine the GCF of 18 and 30. Let's explore the most common and efficient approaches:
1. Listing Factors Method
This is a straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest common factor.
Factors of 18: 1, 2, 3, 6, 9, 18 Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
Common Factors: 1, 2, 3, 6 Greatest Common Factor (GCF): 6
Therefore, the GCF of 18 and 30 is 6. This method is simple but can become cumbersome with larger numbers.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime Factorization of 18: 2 × 3² Prime Factorization of 30: 2 × 3 × 5
Common Prime Factors: 2 and 3 GCF: 2¹ × 3¹ = 6
This method is more efficient than the listing factors method, especially for larger numbers, as it systematically breaks down the numbers into their prime components.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 18 and 30:
- 30 = 18 × 1 + 12 (Subtract 18 from 30, leaving a remainder of 12)
- 18 = 12 × 1 + 6 (Subtract 12 from 18, leaving a remainder of 6)
- 12 = 6 × 2 + 0 (Subtract 6 from 12 twice, leaving a remainder of 0)
The last non-zero remainder is 6, therefore, the GCF of 18 and 30 is 6. This algorithm is remarkably efficient and avoids the need to list all factors or find prime factorizations.
Real-World Applications of GCF
The GCF isn't just a theoretical concept; it has numerous practical applications:
-
Baking: If you have 18 apples and 30 oranges, and you want to make fruit baskets with an equal number of each fruit in each basket, you need to find the GCF of 18 and 30 to determine the maximum number of baskets you can make (6 baskets).
-
Gardening: You have two rectangular garden plots, one measuring 18 feet by 30 feet and the other measuring different dimensions. You want to divide them into identical smaller square plots without any leftover space. The side length of the largest possible square plot is given by the GCF of 18 and 30, which is 6 feet.
-
Construction: Imagine you're tiling a floor with two differently sized rectangular tiles, where one tile measures 18 inches by 18 inches, and another measures 30 inches by 30 inches. To ensure the tiles align perfectly, you'd want to find the largest tile size that will perfectly fit both, given by the GCF of 18 and 30 (6 inches).
-
Resource Allocation: Distributing resources evenly among groups or individuals often involves finding the GCF. If you have 18 pencils and 30 pens and you want to divide them equally among students, the GCF will give you the maximum number of students you can accommodate while ensuring each student receives the same number of pencils and pens.
Expanding the Concept: GCF of More Than Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors raised to their lowest power. For the Euclidean algorithm, you can iteratively find the GCF of two numbers at a time, until you arrive at the GCF of all the numbers.
For example, let's find the GCF of 18, 30, and 42:
- Prime Factorization of 18: 2 × 3²
- Prime Factorization of 30: 2 × 3 × 5
- Prime Factorization of 42: 2 × 3 × 7
The only common prime factor is 2 and 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3¹. Therefore, the GCF of 18, 30, and 42 is 2 × 3 = 6.
Conclusion: Mastering the GCF
The greatest common factor is a fundamental concept in mathematics with numerous practical applications. Understanding the different methods for finding the GCF, from listing factors to employing the efficient Euclidean algorithm, equips you with valuable tools for solving various mathematical problems and tackling real-world scenarios. This guide has provided a detailed explanation of how to determine the GCF, particularly for the numbers 18 and 30, demonstrating its importance across diverse fields. Mastering this concept opens doors to a deeper understanding of number theory and its significant role in numerous practical applications. Remember, the key is choosing the most efficient method based on the size and nature of the numbers involved.
Latest Posts
Latest Posts
-
Excuses Are A Tool Of The Incompetent Poem
May 10, 2025
-
How Much Is 6 Litres Of Water
May 10, 2025
-
What Episode Does Elena Find Out About Vampires
May 10, 2025
-
If I Am 16 When Was I Born
May 10, 2025
-
Is Tim Mcgraw And Faith Hill Getting A Divorce
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor For 18 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.