What Is The Greatest Common Factor For 4 And 8
Arias News
May 10, 2025 · 6 min read
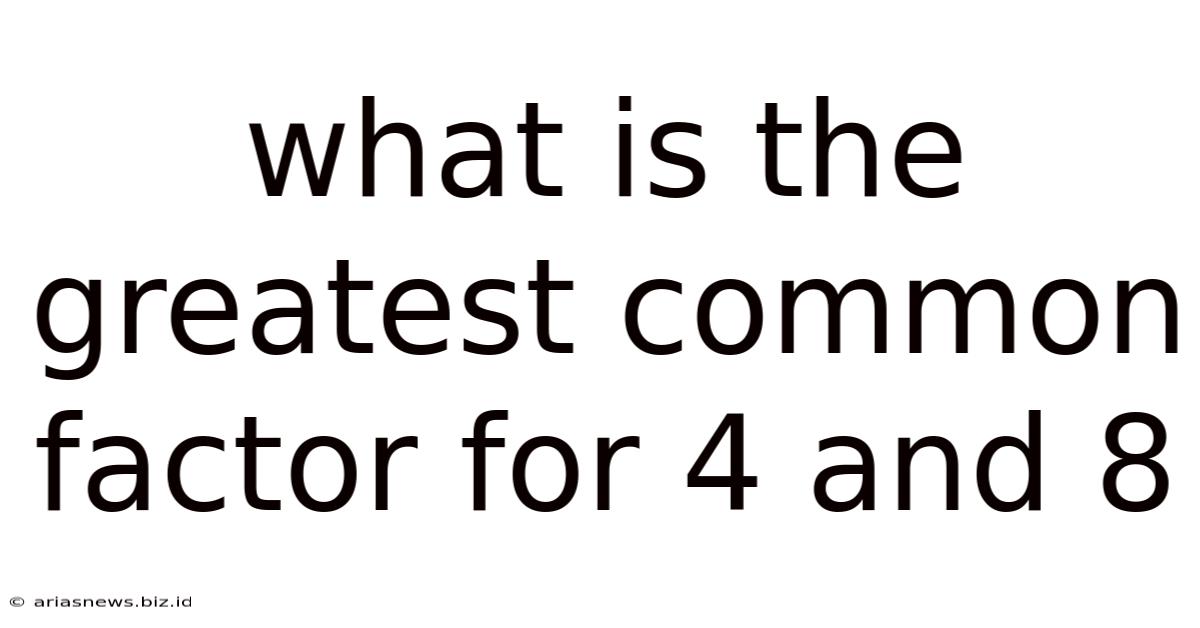
Table of Contents
What is the Greatest Common Factor for 4 and 8? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a deeper appreciation of number theory and its applications in various fields. This article will explore the GCF of 4 and 8, demonstrating different methods for calculation and showcasing the broader significance of this concept in mathematics and beyond.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding the relationships between numbers.
Why is finding the GCF important?
The GCF has numerous applications, including:
-
Simplifying Fractions: Reducing fractions to their simplest form requires finding the GCF of the numerator and denominator. For example, the fraction 8/4 can be simplified to 2/1 (or simply 2) because the GCF of 8 and 4 is 4.
-
Solving Algebraic Equations: GCF is crucial in factoring polynomials, a key technique in solving algebraic equations. Factoring involves expressing a polynomial as a product of its factors, and the GCF is often the first step in this process.
-
Understanding Number Relationships: The GCF reveals insights into the relationships between numbers. For instance, knowing the GCF helps determine if two numbers are relatively prime (meaning their GCF is 1).
-
Real-world Applications: GCF concepts appear in various real-world scenarios, from dividing resources equally to optimizing layouts in design and engineering.
Calculating the GCF of 4 and 8: Multiple Methods
Several methods exist for calculating the greatest common factor. Let's explore the most common approaches to find the GCF of 4 and 8:
Method 1: Listing Factors
This is a straightforward method, especially suitable for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 4: 1, 2, 4 Factors of 8: 1, 2, 4, 8
The common factors are 1, 2, and 4. The largest of these is 4. Therefore, the GCF of 4 and 8 is 4.
Method 2: Prime Factorization
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to the lowest power.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 8: 2 x 2 x 2 = 2³
The only common prime factor is 2. The lowest power of 2 present in both factorizations is 2². Therefore, the GCF is 2² = 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for larger numbers. It's based on repeated division until the remainder is 0. The last non-zero remainder is the GCF.
- Divide the larger number (8) by the smaller number (4): 8 ÷ 4 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last divisor, which is 4.
This method demonstrates the elegance and efficiency of the Euclidean algorithm, especially when dealing with larger numbers where listing factors or prime factorization becomes cumbersome.
Extending the Concept: GCF and Least Common Multiple (LCM)
The greatest common factor is closely related to the least common multiple (LCM). The LCM is the smallest positive integer that is a multiple of both numbers. For 4 and 8:
- Multiples of 4: 4, 8, 12, 16, 20...
- Multiples of 8: 8, 16, 24, 32...
The smallest common multiple is 8. Interestingly, there's a relationship between the GCF and LCM:
GCF(a, b) x LCM(a, b) = a x b
In our case: GCF(4, 8) x LCM(4, 8) = 4 x 8 = 32. This confirms our calculation of the GCF as 4 and the LCM as 8 (since 4 x 8 = 32).
Applications of GCF in Real-World Scenarios
While the concept of GCF might seem purely mathematical, it has practical applications in various real-world situations:
-
Resource Allocation: Imagine you have 12 apples and 16 oranges. You want to create identical gift bags with the maximum number of both fruits in each bag without any leftovers. Finding the GCF of 12 and 16 (which is 4) tells you that you can make 4 identical gift bags, each containing 3 apples and 4 oranges.
-
Construction and Design: GCF is used in determining the optimal size for tiles or bricks when covering a surface area. By finding the GCF of the dimensions of the area and the sizes of the tiles, you can ensure efficient and waste-free tiling.
-
Music Theory: The GCF plays a role in understanding musical intervals and harmonies. Finding the GCF of the frequencies of two notes helps determine their harmonic relationship.
-
Computer Science: The GCF is used in algorithms for data compression, cryptography, and other computational tasks. Efficient GCF algorithms are crucial for the performance of these applications.
-
Scheduling Problems: GCF helps solve scheduling problems where events need to occur at regular intervals. Finding the GCF of the intervals helps determine the next time all events coincide.
Beyond the Basics: Advanced Concepts Related to GCF
The concept of GCF extends beyond simple arithmetic into more advanced areas of mathematics:
-
Modular Arithmetic: GCF is fundamental in modular arithmetic, a branch of number theory dealing with remainders after division. Concepts like modular inverses and solving congruences heavily rely on the GCF.
-
Abstract Algebra: GCF is generalized in abstract algebra through the concept of the greatest common divisor in rings and ideals. This provides a powerful framework for studying algebraic structures.
-
Cryptography: GCF plays a crucial role in RSA cryptography, a widely used public-key cryptosystem. The security of RSA relies on the difficulty of factoring large numbers, which involves finding the GCF.
Conclusion: The Significance of Understanding GCF
Finding the greatest common factor of 4 and 8, while seemingly elementary, serves as a gateway to understanding broader mathematical concepts. From simplifying fractions to its use in advanced algorithms, the GCF holds significant importance across various fields. Mastering different methods for calculating the GCF equips you with valuable tools for solving mathematical problems and understanding the intricate relationships between numbers. Its applications extend beyond the classroom, showcasing its relevance in everyday life and advanced scientific and technological domains. The seemingly simple task of finding the GCF of 4 and 8 reveals a surprising depth and breadth of mathematical concepts and their real-world applications.
Latest Posts
Latest Posts
-
How Many Bales Of Hay In A Ton
May 11, 2025
-
How Many Months Are In 60 Days
May 11, 2025
-
Can You Drink Water With Food Coloring
May 11, 2025
-
How Many Zeros Does Hundred Thousand Have
May 11, 2025
-
37 Out Of 60 As A Percentage
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor For 4 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.