What Is The Greatest Common Factor Of 10 And 40
Arias News
May 10, 2025 · 6 min read
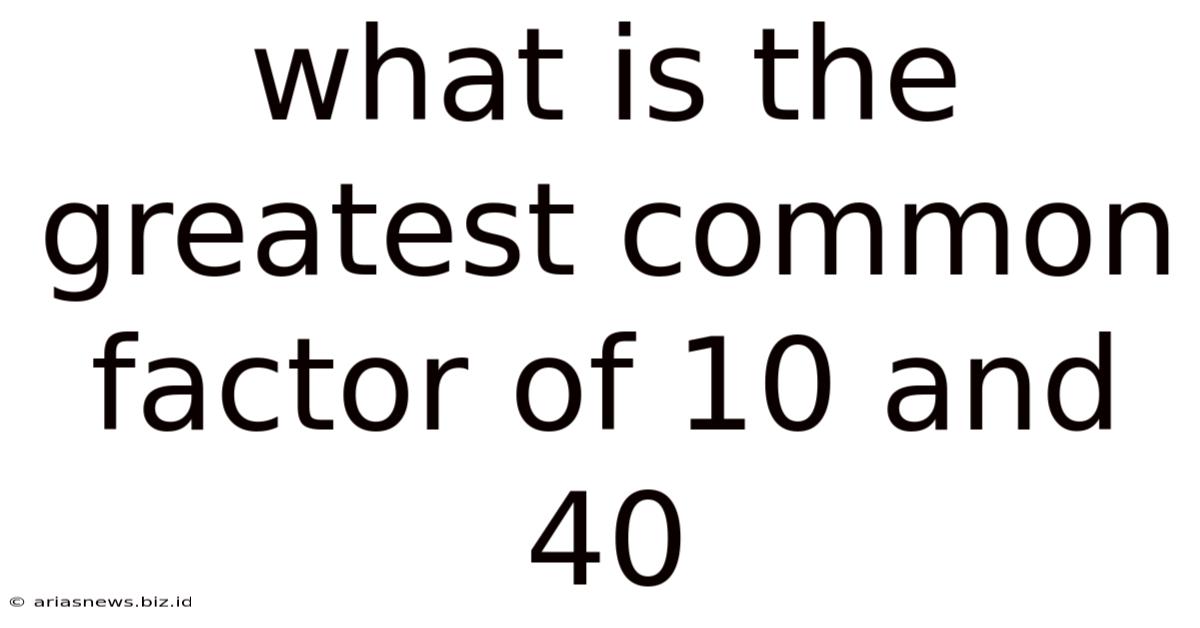
Table of Contents
What is the Greatest Common Factor of 10 and 40? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the concept thoroughly unlocks a deeper appreciation for number theory and its applications in various fields, from cryptography to computer science. This article will not only answer the question, "What is the greatest common factor of 10 and 40?" but also explore the different methods to find the GCF, their underlying principles, and their broader significance in mathematics.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly.
Finding the GCF is a fundamental concept in number theory with practical applications in simplifying fractions, solving algebraic equations, and even in more advanced areas like cryptography and computer programming. Understanding how to efficiently calculate the GCF is crucial for mastering these applications.
Methods for Finding the GCF
Several methods exist for determining the GCF, each with its own advantages and disadvantages depending on the size and nature of the numbers involved. Let's explore some of the most common techniques:
1. Listing Factors Method
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Example: Finding the GCF of 10 and 40
- Factors of 10: 1, 2, 5, 10
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
The common factors are 1, 2, 5, and 10. The greatest of these is 10. Therefore, the GCF of 10 and 40 is 10.
This method works well for small numbers, but it becomes cumbersome and inefficient as the numbers get larger. Finding all the factors of a large number can be time-consuming.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Example: Finding the GCF of 10 and 40 using prime factorization
- Prime factorization of 10: 2 x 5
- Prime factorization of 40: 2<sup>3</sup> x 5
The common prime factors are 2 and 5. The lowest power of 2 is 2<sup>1</sup> (which is 2), and the lowest power of 5 is 5<sup>1</sup> (which is 5). Therefore, the GCF is 2 x 5 = 10.
This method is more efficient than listing factors for larger numbers because it leverages the fundamental building blocks of numbers – prime numbers. However, finding the prime factorization of very large numbers can still be computationally intensive.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Example: Finding the GCF of 10 and 40 using the Euclidean algorithm
- Start with the two numbers: 40 and 10.
- Subtract the smaller number from the larger: 40 - 10 = 30. Now we have 30 and 10.
- Repeat: 30 - 10 = 20. Now we have 20 and 10.
- Repeat: 20 - 10 = 10. Now we have 10 and 10.
- The numbers are equal, so the GCF is 10.
Alternatively, a more efficient version of the Euclidean algorithm uses division instead of subtraction:
- Divide the larger number (40) by the smaller number (10): 40 ÷ 10 = 4 with a remainder of 0.
- Since the remainder is 0, the smaller number (10) is the GCF.
This method is significantly more efficient than the previous methods for larger numbers because it drastically reduces the number of steps required.
Applications of Finding the GCF
The seemingly simple task of finding the greatest common factor has far-reaching applications in various fields:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 40/10 can be simplified to 4/1 (or simply 4) by dividing both the numerator and the denominator by their GCF, which is 10.
-
Solving Diophantine Equations: These are algebraic equations where only integer solutions are sought. The GCF plays a crucial role in determining the solvability and finding the solutions of such equations.
-
Cryptography: The GCF, particularly in the context of the Euclidean algorithm, is fundamental to many cryptographic algorithms. These algorithms rely on the difficulty of finding the GCF of very large numbers to ensure the security of data transmission and storage.
-
Computer Science: The GCF and the Euclidean algorithm are used in various computer algorithms, including those related to data compression, image processing, and computer graphics.
-
Music Theory: The GCF can be used to find the greatest common divisor of the frequencies of two notes, which helps in understanding their harmonic relationships.
-
Geometry: The GCF can be used to determine the side lengths of similar shapes or to simplify ratios in geometric problems.
Beyond Two Numbers: Finding the GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of three numbers (a, b, c), we first find the GCF of any two numbers (say, a and b), and then find the GCF of that result and the remaining number (c). This process can be generalized to any number of integers.
Conclusion: The Power of Simplicity
While finding the GCF of 10 and 40 might seem trivial at first glance, the underlying concepts and methods reveal a fascinating aspect of number theory with surprisingly broad applications. Understanding the different approaches, from simple listing of factors to the elegant Euclidean algorithm, provides valuable insights into the structure of numbers and their relationships. This knowledge is not just academically interesting but also practically useful in various fields, highlighting the power and beauty of seemingly simple mathematical concepts. The GCF, therefore, is far more than just a basic arithmetic operation; it's a cornerstone of numerous mathematical and computational processes that underpin our modern technological world. Mastering this concept unlocks a deeper understanding of the intricate world of numbers and their significant influence on our lives.
Latest Posts
Latest Posts
-
Take A Ride On The Disco Stick
May 11, 2025
-
A Marshmallow Is Cut In Half Physical Or Chemical Change
May 11, 2025
-
Did T D Jakes Wife Leave Him
May 11, 2025
-
What Is The Greatest Common Factor Of 32 And 54
May 11, 2025
-
What Does It Mean When Someone Calls You Sweetheart
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 10 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.