What Is The Greatest Common Factor Of 12a And 9a2
Arias News
May 07, 2025 · 6 min read
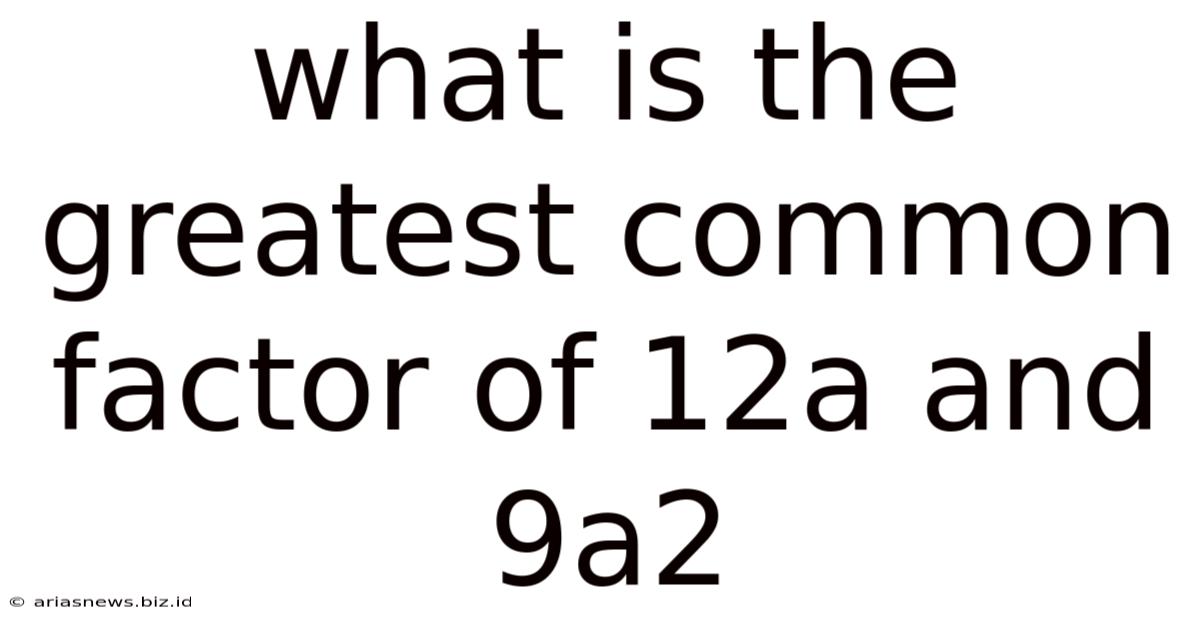
Table of Contents
What is the Greatest Common Factor of 12a and 9a²? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) is a fundamental concept in mathematics, particularly in algebra and number theory. Understanding GCFs is crucial for simplifying expressions, solving equations, and tackling more advanced mathematical problems. This article will explore how to determine the GCF of 12a and 9a², providing a comprehensive explanation along with practical examples and extensions to broader mathematical concepts.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more numbers is the largest number that divides each of them without leaving a remainder. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. The concept extends to algebraic expressions involving variables, as we'll see with 12a and 9a².
Prime Factorization: A Cornerstone Method
A powerful technique for finding the GCF is prime factorization. Prime factorization involves expressing a number as a product of its prime factors – numbers divisible only by 1 and themselves. Let's illustrate this with our example:
- 12a: The prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). Therefore, the prime factorization of 12a is 2² x 3 x a.
- 9a²: The prime factorization of 9 is 3 x 3 (or 3²). The prime factorization of a² is a x a. Therefore, the prime factorization of 9a² is 3² x a².
Once we have the prime factorizations, finding the GCF is straightforward. We identify the common prime factors and their lowest powers present in both factorizations.
In this case:
- Common prime factors: 3 and 'a'
- Lowest powers: 3¹ and a¹
Therefore, the GCF of 12a and 9a² is 3a.
Step-by-Step Calculation of the GCF of 12a and 9a²
Let's break down the process step-by-step to ensure clarity:
-
Factor each term: Find the prime factorization of the numerical coefficients and the variables. As shown above, 12a factors into 2² x 3 x a, and 9a² factors into 3² x a².
-
Identify common factors: Look for the prime factors that appear in both factorizations. In our example, both 12a and 9a² contain the prime factor 3 and the variable 'a'.
-
Determine the lowest power of common factors: For each common factor, select the lowest power present in either factorization. The lowest power of 3 is 3¹ (or simply 3), and the lowest power of 'a' is a¹.
-
Multiply the common factors: Multiply the common factors with their lowest powers together. This gives us 3 x a = 3a.
-
Result: The greatest common factor of 12a and 9a² is 3a.
Applying the GCF in Algebraic Simplification
Understanding GCFs is crucial for simplifying algebraic expressions. For example, consider the expression 12a + 9a². We can factor out the GCF (3a) to simplify the expression:
12a + 9a² = 3a(4 + 3a)
This simplified form is often more manageable and easier to work with in further algebraic manipulations. Factoring out the GCF is a key step in solving equations and simplifying complex expressions.
Extending the Concept: GCF of Polynomials
The concept of GCF extends beyond simple terms like 12a and 9a². We can find the GCF of more complex polynomial expressions. For example, let's consider the polynomials 6x³ + 9x² and 3x².
-
Factor each polynomial: 6x³ + 9x² = 3x²(2x + 3) and 3x² is already in factored form.
-
Identify common factors: Both polynomials contain the factor 3x².
-
The GCF is 3x².
This demonstrates how the GCF can simplify and help manipulate polynomial expressions, enabling easier solutions in polynomial equations and other algebraic calculations.
Finding GCF Using the Euclidean Algorithm
While prime factorization is a reliable method, especially for smaller numbers, the Euclidean Algorithm offers an alternative, particularly useful for larger numbers or when prime factorization becomes computationally intensive. The Euclidean Algorithm is an iterative process based on the property that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number.
Let's illustrate with an example unrelated to our initial problem, finding the GCF of 48 and 18:
-
Start with the larger number (48) and the smaller number (18).
-
Divide the larger number by the smaller number and find the remainder: 48 ÷ 18 = 2 with a remainder of 12.
-
Replace the larger number with the remainder: Now we find the GCF of 18 and 12.
-
Repeat the process: 18 ÷ 12 = 1 with a remainder of 6.
-
Repeat again: 12 ÷ 6 = 2 with a remainder of 0.
-
The last non-zero remainder is the GCF: The GCF of 48 and 18 is 6.
This algorithm is efficient and avoids the need for complete prime factorization, making it valuable for larger numbers. While less intuitive for algebraic expressions with variables, the Euclidean algorithm showcases a powerful alternative approach to finding GCFs.
Real-World Applications of GCFs
The application of GCFs extends beyond theoretical mathematics; it's deeply embedded in various real-world scenarios. Consider these examples:
-
Dividing resources fairly: Imagine you have 12 apples and 9 oranges, and you want to divide them evenly among several people. The GCF (3) determines the maximum number of people you can divide the fruits among evenly without having to split any fruit.
-
Simplifying fractions: Reducing fractions to their simplest form requires finding the GCF of the numerator and denominator. For instance, the fraction 12/18 simplifies to 2/3 after dividing both numerator and denominator by their GCF, which is 6.
-
Project management: Suppose you have two tasks taking 12 hours and 9 hours, respectively. The GCF helps determine the common time intervals for planning and scheduling the project.
-
Construction and engineering: The GCF plays a role in creating precise measurements and proportions in designs, ensuring that materials are used efficiently and measurements align harmoniously.
-
Computer science and cryptography: GCF calculations are fundamental in cryptography for encryption and security protocols.
Conclusion: Mastering GCFs for Mathematical Proficiency
Understanding and applying the greatest common factor is a cornerstone skill in mathematics. Whether dealing with simple numbers, algebraic expressions, or complex polynomials, the ability to find the GCF significantly simplifies calculations and opens doors to more advanced mathematical concepts. This article provides a thorough foundation, equipping you with the knowledge and techniques to confidently tackle GCF problems and apply this crucial concept in diverse mathematical contexts and real-world applications. The choice between prime factorization and the Euclidean algorithm depends on the specific context and the complexity of the numbers or polynomials involved. Mastering both methods provides a flexible and powerful toolkit for navigating the world of GCFs.
Latest Posts
Latest Posts
-
What Is The Average Height For An 8th Grader
May 11, 2025
-
What To Say After Reading Scripture In Church
May 11, 2025
-
How Do You Find The Average Of Fractions
May 11, 2025
-
How Many 1 4 Equal 1 2 Cup
May 11, 2025
-
How To Say I Saw In Spanish
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 12a And 9a2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.