What Is The Greatest Common Factor Of 14 And 49
Arias News
Apr 08, 2025 · 6 min read
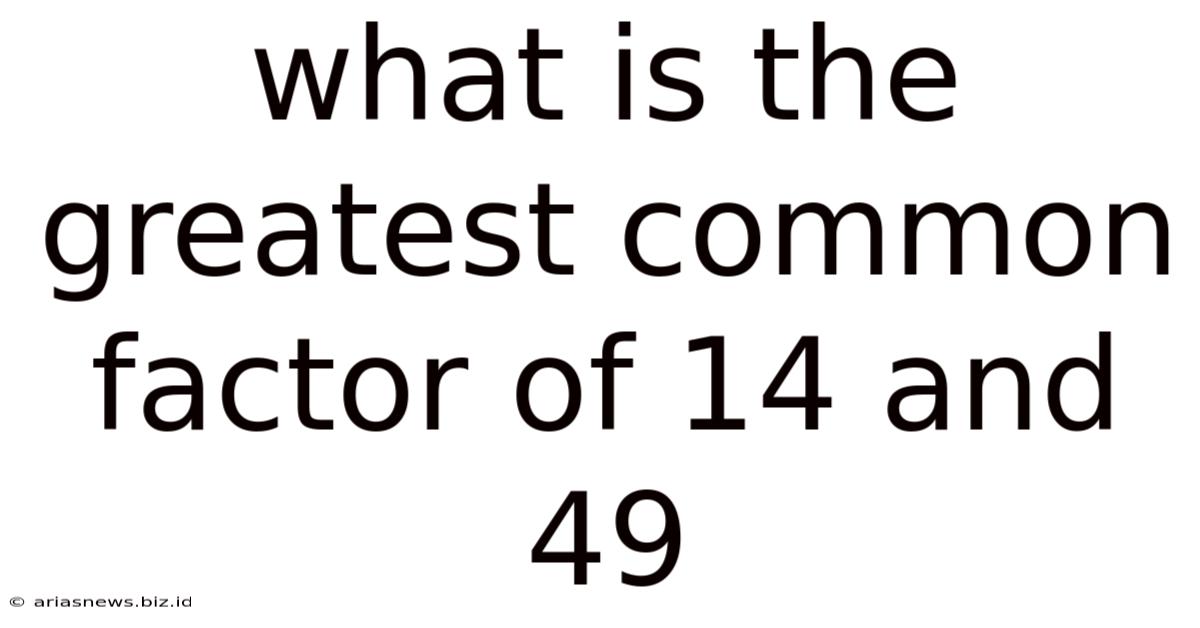
Table of Contents
What is the Greatest Common Factor of 14 and 49? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it's a fundamental concept in number theory with applications far beyond basic mathematics. This article will explore the GCF of 14 and 49, demonstrating various methods to calculate it and then delving into the broader significance of GCFs in algebra, cryptography, and computer science.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 perfectly.
Why is finding the GCF important?
The GCF is a crucial concept in mathematics for several reasons:
- Simplifying fractions: The GCF allows us to simplify fractions to their lowest terms. Dividing both the numerator and denominator by their GCF gives an equivalent fraction in its simplest form.
- Solving algebraic equations: GCFs play a significant role in factoring polynomials, a key step in solving many algebraic equations.
- Cryptography: The GCF, specifically the Euclidean algorithm for finding it, is fundamental to various cryptographic techniques.
- Computer science: Efficient algorithms for calculating the GCF are used in computer science for various applications, including data compression and digital signal processing.
Calculating the GCF of 14 and 49
Now let's tackle the specific problem: finding the GCF of 14 and 49. We can use several methods:
Method 1: Listing Factors
The simplest method is to list all the factors of each number and identify the largest common factor.
- Factors of 14: 1, 2, 7, 14
- Factors of 49: 1, 7, 49
Comparing the lists, we see that the common factors are 1 and 7. The greatest of these is 7. Therefore, the GCF of 14 and 49 is 7.
Method 2: Prime Factorization
This method involves expressing each number as a product of its prime factors. The GCF is then the product of the common prime factors raised to the lowest power.
- Prime factorization of 14: 2 x 7
- Prime factorization of 49: 7 x 7 (or 7²)
The only common prime factor is 7. The lowest power of 7 in either factorization is 7¹. Therefore, the GCF is 7.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a more efficient method, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
- Start with the larger number (49) and the smaller number (14).
- Divide 49 by 14: 49 ÷ 14 = 3 with a remainder of 7.
- Replace the larger number (49) with the remainder (7). Now we have 14 and 7.
- Divide 14 by 7: 14 ÷ 7 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 7.
The Euclidean algorithm is particularly efficient for very large numbers because it avoids the need to find all factors.
Applications of GCF in Different Fields
The seemingly simple concept of the GCF has far-reaching applications in diverse fields:
1. Simplifying Fractions in Mathematics
As mentioned earlier, finding the GCF is crucial for simplifying fractions. For example, the fraction 14/49 can be simplified by dividing both the numerator and the denominator by their GCF (7), resulting in the equivalent fraction 2/7. This simplification makes fractions easier to understand and manipulate.
2. Factoring Polynomials in Algebra
In algebra, the GCF plays a vital role in factoring polynomials. Factoring is the process of expressing a polynomial as a product of simpler polynomials. Finding the GCF of the terms in a polynomial allows us to factor out the common terms, simplifying the polynomial and making it easier to solve equations or analyze its properties. For example, consider the polynomial 14x² + 49x. The GCF of 14x² and 49x is 7x. Therefore, we can factor the polynomial as 7x(2x + 7).
3. Cryptography and Security
The Euclidean algorithm, used for finding the GCF, forms the foundation of several cryptographic algorithms. These algorithms are crucial for securing online communication and data transmission. The RSA algorithm, a widely used public-key cryptosystem, heavily relies on the difficulty of finding the GCF of two very large numbers, making it computationally infeasible to break the encryption.
4. Computer Science and Algorithms
Efficient algorithms for computing the GCF are vital in various computer science applications. The Euclidean algorithm, for instance, is highly efficient and forms the basis of several other algorithms. These algorithms are utilized in:
- Data compression: GCF calculations help optimize data compression techniques by identifying common factors within data sets.
- Digital signal processing: GCFs are utilized in signal processing for tasks such as noise reduction and signal analysis.
- Computer graphics: Certain aspects of computer graphics, particularly in texture generation and manipulation, might use GCF-based algorithms for efficient processing.
Beyond the Basics: Exploring Related Concepts
The concept of the GCF opens the door to understanding more advanced mathematical concepts:
- Least Common Multiple (LCM): The LCM of two integers is the smallest positive integer that is divisible by both integers. The GCF and LCM are related: the product of the GCF and LCM of two numbers is equal to the product of the two numbers.
- Modular Arithmetic: Modular arithmetic deals with remainders after division. The GCF is frequently used in solving congruences and other problems in modular arithmetic.
- Diophantine Equations: These are algebraic equations where only integer solutions are sought. The GCF often plays a critical role in determining whether a Diophantine equation has solutions and finding those solutions.
Conclusion: The Unsung Power of the GCF
While initially appearing as a simple arithmetic operation, calculating the greatest common factor reveals a surprising depth of mathematical significance. From simplifying fractions to securing online communications, the GCF underpins many critical applications across diverse fields. Understanding the GCF and its associated algorithms is not just a matter of academic interest; it's a fundamental skill with practical implications in mathematics, computer science, and cryptography, shaping our technological world in profound ways. The seemingly straightforward task of finding the GCF of 14 and 49—which we've determined to be 7—serves as a gateway to a richer understanding of number theory and its widespread influence.
Latest Posts
Latest Posts
-
Can You Pass A Class With A D
Apr 17, 2025
-
Size 6 In Womens To Mens Pants
Apr 17, 2025
-
How Did Derwin Find Out About Melanie And The Doctor
Apr 17, 2025
-
How Many Feet Of Starter Shingles In A Bundle
Apr 17, 2025
-
What Is Long And Yellow And Never Rings
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 14 And 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.