What Is The Greatest Common Factor Of 18 And 27
Arias News
May 08, 2025 · 5 min read
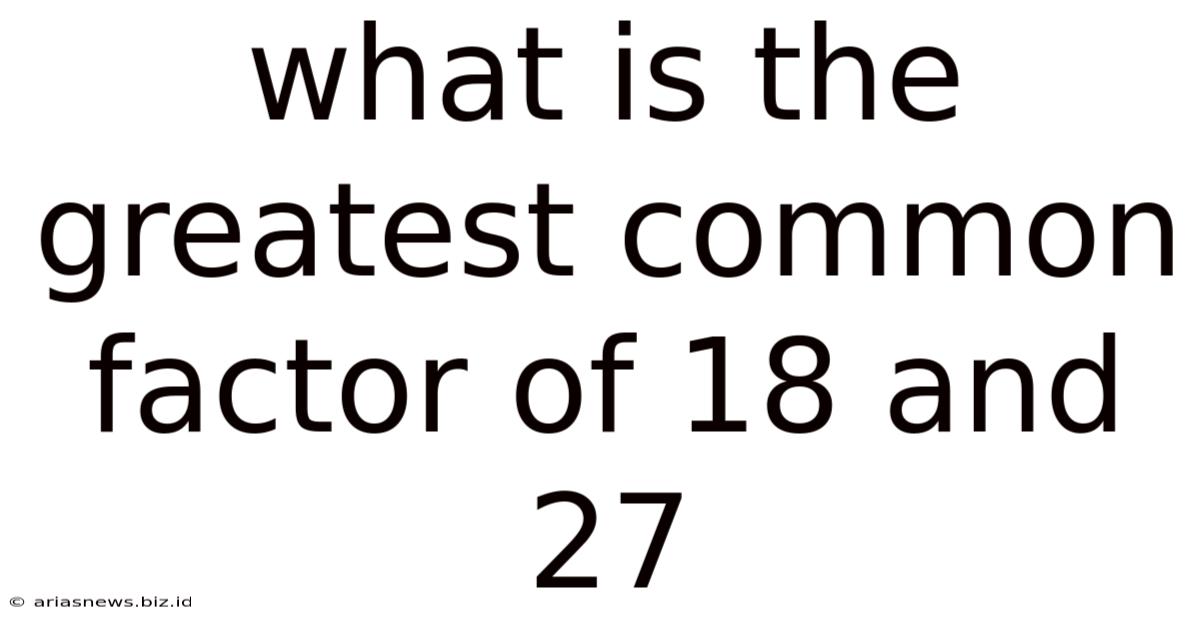
Table of Contents
What is the Greatest Common Factor of 18 and 27? A Deep Dive into Finding GCFs
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can unlock a deeper appreciation of number theory and its applications. This article will delve into the question: What is the greatest common factor of 18 and 27? We'll not only find the answer but also explore various techniques to determine GCFs, discuss their significance in mathematics and beyond, and provide you with the tools to tackle similar problems with confidence.
Understanding Greatest Common Factors
Before jumping into the specifics of 18 and 27, let's establish a clear understanding of what a greatest common factor represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. It's also known as the greatest common divisor (GCD). This seemingly simple concept plays a crucial role in various mathematical operations and real-world applications.
For instance, imagine you have 18 red marbles and 27 blue marbles. You want to divide them into identical bags, with each bag containing the same number of red and blue marbles. To determine the maximum number of bags you can create, you need to find the GCF of 18 and 27. This will tell you the largest number of marbles of each color that can be placed in each bag.
Method 1: Prime Factorization
The most fundamental method for finding the GCF is prime factorization. This involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves. Let's apply this method to 18 and 27:
18:
- 18 = 2 x 9
- 18 = 2 x 3 x 3
- 18 = 2 x 3²
27:
- 27 = 3 x 9
- 27 = 3 x 3 x 3
- 27 = 3³
Now, let's identify the common prime factors: both 18 and 27 share three 3s as factors. Therefore, the GCF is 3 x 3 = 9.
Therefore, the greatest common factor of 18 and 27 is 9.
Method 2: Listing Factors
Another straightforward approach is to list all the factors of each number and identify the largest common factor.
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 27: 1, 3, 9, 27
By comparing the two lists, we observe that the common factors are 1, 3, and 9. The largest of these is 9, confirming our previous result. This method works well for smaller numbers, but it can become less efficient as numbers grow larger.
Method 3: Euclidean Algorithm
For larger numbers, the Euclidean algorithm provides a more efficient method. This algorithm is based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. Let's illustrate with 18 and 27:
- Start with the larger number (27) and the smaller number (18).
- Subtract the smaller number from the larger number: 27 - 18 = 9
- Replace the larger number with the result (9) and repeat the process. Now we have 18 and 9.
- Subtract the smaller number from the larger number: 18 - 9 = 9
- The process stops when the result is 0. In this case, we have 9 and 9, and 9 - 9 = 0.
The last non-zero remainder (which is 9) is the GCF. The Euclidean algorithm is particularly useful for larger numbers where listing factors might be cumbersome.
The Significance of GCFs
The concept of the greatest common factor extends far beyond simple arithmetic exercises. GCFs have significant applications in various fields:
- Simplification of Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For example, the fraction 18/27 can be simplified to 2/3 by dividing both the numerator and denominator by their GCF (9).
- Algebraic Expressions: GCFs are crucial in factoring algebraic expressions. Finding the GCF of terms allows us to simplify and solve equations more efficiently.
- Geometry: GCFs can be used to solve problems involving area and volume calculations. For example, finding the GCF of the dimensions of a rectangular prism helps determine the size of the largest cube that can evenly fill the prism.
- Real-world Applications: The marble example we discussed earlier illustrates a practical application. GCFs are also used in scheduling, resource allocation, and other areas where efficient division is needed.
Exploring Further: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. For 18 and 27, the LCM can be found using the prime factorization method or other techniques.
- Prime Factorization: 18 = 2 x 3² and 27 = 3³. The LCM includes the highest power of each prime factor present in either number: 2 x 3³ = 54.
- Formula relating GCF and LCM: There's a useful relationship between the GCF and LCM of two numbers (a and b): GCF(a, b) x LCM(a, b) = a x b. Using this, since GCF(18, 27) = 9 and 18 x 27 = 486, we can calculate the LCM as 486 / 9 = 54.
Conclusion: Mastering GCFs and Their Applications
This in-depth exploration clarifies that the greatest common factor of 18 and 27 is 9. We've examined three different methods for finding the GCF – prime factorization, listing factors, and the Euclidean algorithm – each offering different advantages depending on the context. Understanding GCFs isn't just about performing a calculation; it's about grasping a fundamental concept with widespread applications across mathematics and beyond. By mastering these techniques and appreciating their significance, you'll develop a stronger foundation in number theory and enhance your problem-solving abilities in various fields. Remember, the seemingly simple act of finding the GCF unlocks a world of mathematical possibilities.
Latest Posts
Latest Posts
-
What Is The Function Of Monitor In Computer
May 09, 2025
-
How Do You Say Mcdonalds In Spanish
May 09, 2025
-
How Many Ounces In 2 Pounds Of Ground Beef
May 09, 2025
-
Kala Shah Kala Song Meaning In English
May 09, 2025
-
How To Say Bless You In Hawaiian
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 18 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.