What Is The Greatest Common Factor Of 30 And 18
Arias News
May 09, 2025 · 6 min read
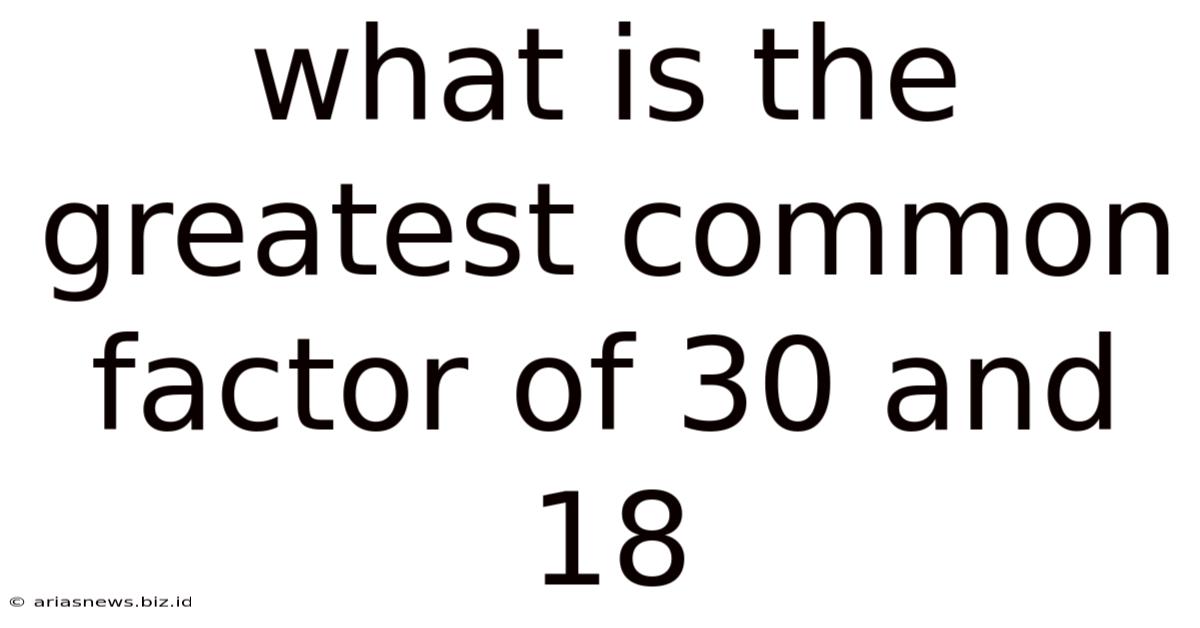
Table of Contents
What is the Greatest Common Factor of 30 and 18? A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and exploring different methods for calculating the GCF opens a window into fascinating aspects of number theory, with applications far beyond basic arithmetic. This article will not only answer the question – what is the greatest common factor of 30 and 18? – but will also delve into the various approaches to solving this problem and explore its broader mathematical significance.
Understanding the Concept of Greatest Common Factor
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding various mathematical structures.
Why is the GCF Important?
The GCF has significant implications across various mathematical areas:
-
Simplifying Fractions: The GCF allows us to reduce fractions to their simplest form. For example, the fraction 18/30 can be simplified by dividing both the numerator and denominator by their GCF.
-
Algebraic Expressions: The GCF is crucial when factoring algebraic expressions. Finding the GCF of the terms allows us to simplify and solve equations more efficiently.
-
Number Theory: The GCF is a cornerstone concept in number theory, forming the basis for many advanced theorems and algorithms.
-
Real-World Applications: The GCF finds applications in various real-world scenarios, such as dividing objects into equal groups, determining the size of the largest square tile that can fit perfectly into a rectangular area, and optimizing resource allocation.
Methods for Finding the Greatest Common Factor
Several methods exist for determining the GCF of two numbers. Let's explore some of the most common and effective techniques.
1. Listing Factors Method
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30 Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1, 2, 3, and 6. The greatest of these is 6. Therefore, the GCF of 30 and 18 is 6.
This method becomes cumbersome for larger numbers with numerous factors.
2. Prime Factorization Method
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime factorization of 30: 2 x 3 x 5 Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCF is 2 x 3 = 6.
This method is efficient for relatively small numbers but can also become challenging for very large numbers.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It relies on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal. That equal number is the GCF.
Let's apply the Euclidean algorithm to 30 and 18:
- 30 = 1 x 18 + 12 (Subtract 18 from 30, the remainder is 12)
- 18 = 1 x 12 + 6 (Subtract 12 from 18, the remainder is 6)
- 12 = 2 x 6 + 0 (Subtract 6 from 12, the remainder is 0)
The last non-zero remainder is 6, which is the GCF of 30 and 18. The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers.
Answering the Question: What is the GCF of 30 and 18?
Using any of the methods described above (listing factors, prime factorization, or the Euclidean algorithm), we consistently arrive at the same answer: The greatest common factor of 30 and 18 is 6.
Extending the Concept: GCF of More Than Two Numbers
The concept of GCF can be extended to find the greatest common factor of more than two numbers. The methods described above can be adapted for this purpose. For instance, using prime factorization, we would find the prime factorization of each number and then select the common prime factors raised to their lowest power. The Euclidean algorithm can also be extended to handle more than two numbers, though the process becomes slightly more complex.
Applications of GCF in Real-World Scenarios
The GCF is not merely an abstract mathematical concept; it has practical applications in various real-world situations:
-
Dividing Objects into Equal Groups: Imagine you have 30 apples and 18 oranges. You want to divide them into equal groups, with each group containing the same number of apples and oranges. The GCF (6) tells you that you can create 6 groups, each with 5 apples and 3 oranges.
-
Tiling Problems: Suppose you want to tile a rectangular floor that measures 30 feet by 18 feet using square tiles of equal size. The largest square tile you can use without cutting any tiles is a tile with side length equal to the GCF (6 feet).
-
Recipe Scaling: Imagine you have a recipe that requires 30 grams of flour and 18 grams of sugar. If you want to reduce the recipe, you can divide both amounts by their GCF (6) to obtain a smaller but proportionally equivalent recipe.
-
Simplifying Ratios: Ratios can be simplified using the GCF. For instance, a ratio of 30:18 can be simplified to 5:3 by dividing both numbers by their GCF (6).
Conclusion
Finding the greatest common factor of 30 and 18, which is 6, is more than a simple arithmetic exercise. It illustrates fundamental concepts within number theory and demonstrates the power and efficiency of various algorithms. Understanding the GCF unlocks the ability to simplify fractions, factor algebraic expressions, and solve practical problems in various contexts. The methods discussed—listing factors, prime factorization, and the Euclidean algorithm—each offer a unique approach to finding the GCF, with the Euclidean algorithm proving particularly efficient for larger numbers. The widespread applications of the GCF in diverse fields highlight its importance as a fundamental concept in mathematics and its practical relevance in everyday life. The seemingly simple question of finding the GCF opens up a wide world of mathematical exploration and practical problem-solving.
Latest Posts
Latest Posts
-
How Much Is 2 Ounces Of Cheese
May 09, 2025
-
How Long Is An Acre In Yards
May 09, 2025
-
What Did Thomas Gainsborough And Gilbert Stuart Have In Common
May 09, 2025
-
How Many Cups Is One Bell Pepper
May 09, 2025
-
Do Peahens Lay Eggs Without A Mate
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 30 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.