What Is The Lcm Of 2 And 9
Arias News
May 10, 2025 · 5 min read
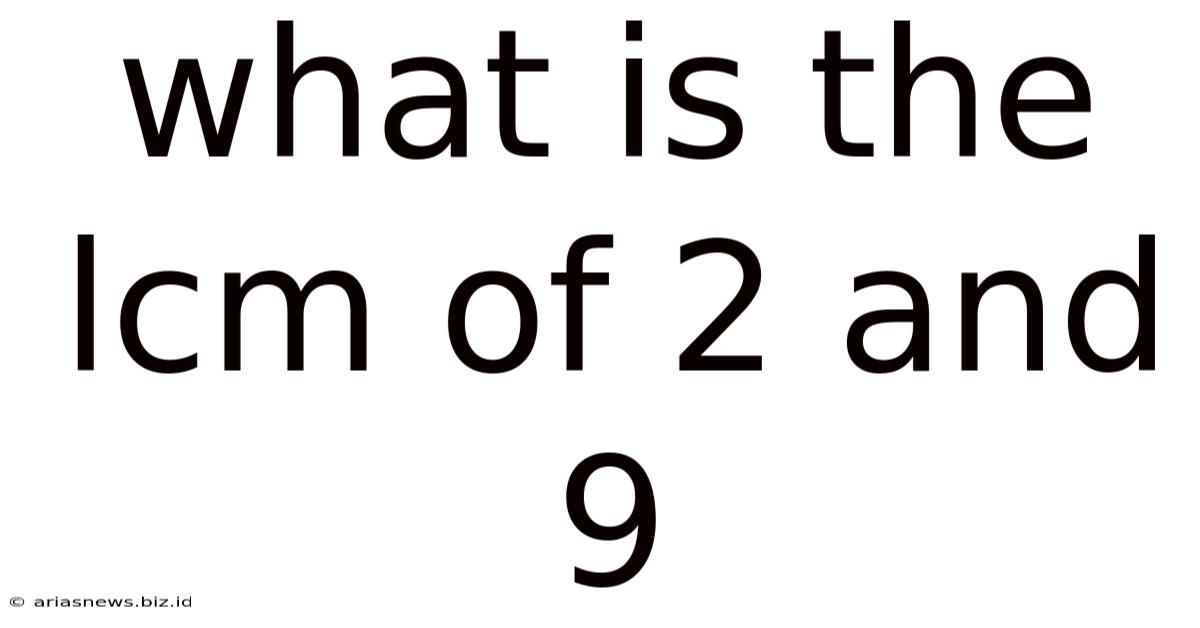
Table of Contents
What is the LCM of 2 and 9? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can unlock a deeper appreciation for number theory. This article will delve into the question, "What is the LCM of 2 and 9?", providing not just the answer but a comprehensive exploration of LCMs, their applications, and various calculation methods. We’ll also touch upon the relationship between LCM and greatest common divisor (GCD), broadening our understanding of fundamental mathematical concepts.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that is a multiple of each of the given numbers. For example, the multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20… and the multiples of 9 are 9, 18, 27, 36, 45… The smallest number that appears in both lists is 18; therefore, the LCM of 2 and 9 is 18.
Why are LCMs Important?
LCMs have numerous applications in various fields, including:
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator, simplifying the calculation.
-
Scheduling Problems: LCMs are essential in solving scheduling problems. For instance, if two events occur at different intervals (e.g., buses arriving every 2 hours and trains every 9 hours), finding the LCM helps determine when both events will occur simultaneously.
-
Modular Arithmetic: In cryptography and computer science, LCMs play a critical role in modular arithmetic operations.
-
Music Theory: Understanding LCMs aids in the analysis and composition of music, especially concerning rhythmic patterns and harmonic structures.
Calculating the LCM of 2 and 9: Different Methods
Several methods can be used to calculate the LCM of 2 and 9. Let's explore some of the most common ones:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 9: 9, 18, 27, 36...
As we can see, the smallest number that appears in both lists is 18. Therefore, the LCM(2, 9) = 18.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present in either factorization.
- Prime factorization of 2: 2¹
- Prime factorization of 9: 3²
To find the LCM, we take the highest power of each prime factor present: 2¹ and 3². Multiplying these together, we get: 2¹ * 3² = 2 * 9 = 18. Therefore, the LCM(2, 9) = 18.
3. Using the GCD (Greatest Common Divisor)
The LCM and GCD are closely related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 2 and 9 using the Euclidean algorithm:
- Divide 9 by 2: 9 = 2 * 4 + 1
- Divide 2 by 1: 2 = 1 * 2 + 0
The GCD is the last non-zero remainder, which is 1.
Now, using the formula:
LCM(2, 9) * GCD(2, 9) = 2 * 9 LCM(2, 9) * 1 = 18 LCM(2, 9) = 18
This method confirms that the LCM of 2 and 9 is indeed 18.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, we consider all prime factors from all numbers and take the highest power of each. For the listing multiples method, it becomes more cumbersome but still feasible for relatively small numbers. The GCD method can also be extended using iterative applications of the GCD and LCM relationship.
Practical Applications: Real-World Examples
Let's illustrate the practical application of LCMs with some real-world scenarios:
Scenario 1: Scheduling a Meeting
Two colleagues, Alex and Ben, want to schedule a meeting. Alex is available every 2 days, and Ben is available every 9 days. To find the earliest day they are both available, we need to find the LCM of 2 and 9, which is 18. They will both be available for a meeting on the 18th day.
Scenario 2: Fraction Addition
Suppose we need to add the fractions 1/2 and 1/9. To do this, we need a common denominator. The LCM of 2 and 9 is 18. We rewrite the fractions as 9/18 and 2/18, allowing us to add them easily: 9/18 + 2/18 = 11/18.
Scenario 3: Rhythmic Patterns in Music
Imagine a musical piece with two rhythmic patterns: one repeating every 2 beats and another repeating every 9 beats. The LCM of 2 and 9 (18) indicates that both patterns will align perfectly every 18 beats.
Conclusion: Mastering the LCM
Understanding the LCM is fundamental in various mathematical and real-world applications. Whether using the listing multiples method, prime factorization, or the GCD relationship, calculating the LCM efficiently is a valuable skill. This article has explored different approaches, highlighting their strengths and weaknesses, equipping you with a solid understanding of how to find the LCM of two (or more) numbers. Remember, the key is to choose the most efficient method based on the numbers involved, and always double-check your calculations to ensure accuracy. The LCM of 2 and 9, as demonstrated through multiple methods, is definitively 18. This seemingly simple concept forms a cornerstone of more complex mathematical ideas and problem-solving techniques.
Latest Posts
Latest Posts
-
How Do You Say Daddy In Hebrew
May 10, 2025
-
Vowel Sound Represented By An Upside Down
May 10, 2025
-
A Small Amount Of Something Like Seasoning For Food
May 10, 2025
-
How Many Quarts In A 9x9 Baking Dish
May 10, 2025
-
How Much Is 2 Miles In Minutes
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 2 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.