What Is The Lcm Of 3 5 And 11
Arias News
May 12, 2025 · 5 min read
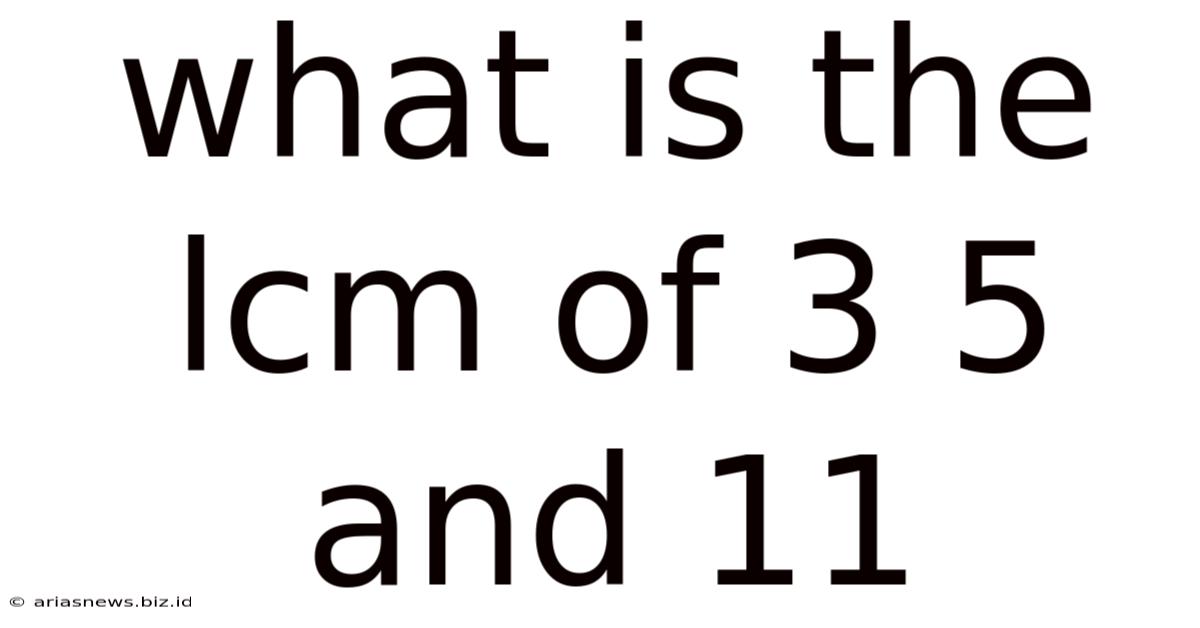
Table of Contents
What is the LCM of 3, 5, and 11? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, with applications ranging from simple fraction arithmetic to complex scheduling problems. This article will thoroughly explore how to determine the LCM of 3, 5, and 11, while also providing a broader understanding of LCM calculations and their practical uses. We'll cover various methods, explain the underlying principles, and illustrate the process step-by-step.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 3, 5, and 11, let's establish a solid understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is 6.
Method 1: Listing Multiples
The simplest method, suitable for smaller numbers like 3, 5, and 11, involves listing the multiples of each number until a common multiple is found.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 111, 114, 117, 120, 132, 143, 156, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155, 160, 165, ...
- Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165, ...
By comparing these lists, we can see that the smallest common multiple is 165. Therefore, the LCM(3, 5, 11) = 165. This method is straightforward but becomes less efficient with larger numbers.
Method 2: Prime Factorization
A more efficient and systematic method for finding the LCM involves using prime factorization. This method is particularly useful when dealing with larger numbers or a greater number of integers.
Step 1: Find the prime factorization of each number.
- 3 = 3 (3 is a prime number)
- 5 = 5 (5 is a prime number)
- 11 = 11 (11 is a prime number)
Step 2: Identify the highest power of each prime factor.
In this case, each prime factor (3, 5, and 11) appears only once, raised to the power of 1.
Step 3: Multiply the highest powers of all prime factors together.
LCM(3, 5, 11) = 3¹ × 5¹ × 11¹ = 3 × 5 × 11 = 165
Therefore, the LCM of 3, 5, and 11 is 165. This method is more elegant and scalable than the method of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) × GCD(a, b) = a × b
This formula can be extended to more than two numbers. However, calculating the GCD for multiple numbers can be complex. For three numbers, it requires a multi-step process. While this method is mathematically sound, for the specific case of 3, 5, and 11, the prime factorization method is significantly simpler.
Applications of LCM
The concept of LCM has numerous applications across various fields:
1. Fraction Arithmetic: Finding a Common Denominator**
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator. This simplifies the calculation process.
2. Scheduling Problems: Finding Overlapping Events**
Imagine two events that occur cyclically. One event happens every 3 days, another every 5 days, and a third every 11 days. The LCM helps determine when all three events will occur simultaneously. In our example, they'll coincide every 165 days.
3. Gear Ratios and Mechanical Systems**
In engineering, the LCM is used in designing gear ratios and other mechanical systems where cyclical movements need to be synchronized.
4. Music Theory: Harmonizing Musical Intervals**
The LCM is used to determine the least common multiple of the periods or frequencies of different musical notes. This is important for creating harmonious chords and understanding musical intervals.
5. Abstract Algebra and Number Theory**
LCM is a fundamental concept in abstract algebra and number theory and is used in various advanced mathematical proofs and theorems.
Conclusion: The Power of the LCM
The least common multiple is a seemingly simple mathematical concept, yet its applications are surprisingly diverse and far-reaching. Understanding how to calculate the LCM, particularly through efficient methods like prime factorization, is a valuable skill for anyone working with numbers, whether in basic arithmetic, advanced mathematics, or real-world applications. We've demonstrated that the LCM of 3, 5, and 11 is 165 using multiple methods, highlighting the versatility and importance of this core mathematical concept. Hopefully, this detailed exploration has provided a comprehensive understanding of LCM and its significance. Remember to choose the method best suited to your needs and the complexity of the numbers involved.
Latest Posts
Latest Posts
-
How Much Is 33 Celsius In Fahrenheit
May 12, 2025
-
The Distance Around A Figure Is The
May 12, 2025
-
How Do You Say A Pencil In Spanish
May 12, 2025
-
Does Tropicana Orange Juice Need To Be Refrigerated
May 12, 2025
-
Bear Creek Potato Soup In Crock Pot
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 5 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.