What Is The Lcm Of 3 6 And 10
Arias News
May 11, 2025 · 5 min read
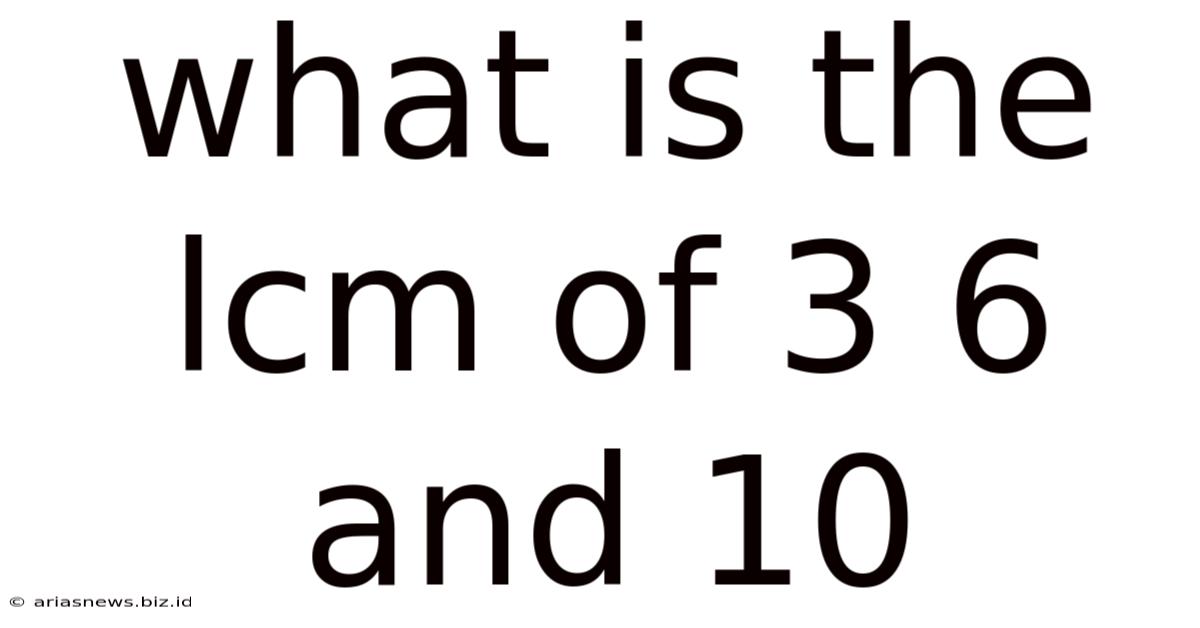
Table of Contents
What is the LCM of 3, 6, and 10? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic problem, but understanding the underlying concepts and different methods for calculating it is crucial for various mathematical applications. This comprehensive guide will delve into the process of determining the LCM of 3, 6, and 10, explaining multiple approaches and demonstrating their practical uses. We'll explore the fundamental principles behind LCMs and highlight why this seemingly basic concept is vital in fields ranging from simple fraction addition to complex scheduling problems.
Understanding Least Common Multiples (LCM)
Before jumping into the calculation, let's solidify our understanding of LCMs. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. Think of it as the smallest number that contains all the numbers in your set as factors.
For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21...
The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is 6.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers like 3, 6, and 10. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 10: 10, 20, 30, 40...
By comparing the lists, we observe that the smallest number appearing in all three lists is 30. Therefore, the LCM of 3, 6, and 10 is 30.
This method is simple for small numbers but becomes cumbersome and inefficient when dealing with larger numbers or a greater quantity of numbers.
Method 2: Prime Factorization
Prime factorization is a more robust and efficient method for finding the LCM, especially when dealing with larger numbers. It involves breaking down each number into its prime factors. A prime factor is a number that is only divisible by 1 and itself (e.g., 2, 3, 5, 7, 11...).
Let's prime factorize 3, 6, and 10:
- 3 = 3 (3 is a prime number)
- 6 = 2 x 3
- 10 = 2 x 5
Now, to find the LCM, we take the highest power of each prime factor present in the factorization of the numbers:
- The prime factors present are 2, 3, and 5.
- The highest power of 2 is 2<sup>1</sup> = 2.
- The highest power of 3 is 3<sup>1</sup> = 3.
- The highest power of 5 is 5<sup>1</sup> = 5.
Multiplying these highest powers together gives us the LCM: 2 x 3 x 5 = 30.
This method is significantly more efficient than listing multiples, especially when working with larger numbers. It provides a systematic and reliable approach to finding the LCM.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides all the given numbers without leaving a remainder. We can use the following formula to relate LCM and GCD:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
First, let's find the GCD of 3, 6, and 10. The GCD of these numbers is 1 (as they don't share any common factors other than 1).
Now, we can use the formula:
LCM(3, 6, 10) = (3 x 6 x 10) / GCD(3, 6, 10) = 180 / 1 = 30
This method requires calculating the GCD first, which can be done using various techniques like the Euclidean algorithm. However, for smaller numbers, this method might not be significantly more efficient than prime factorization.
Practical Applications of LCM
The concept of LCM finds applications in various real-world scenarios:
1. Fraction Addition and Subtraction:
Finding a common denominator when adding or subtracting fractions is directly related to finding the LCM of the denominators. For example, to add 1/3 + 1/6 + 1/10, we need to find the LCM of 3, 6, and 10, which is 30. This allows us to rewrite the fractions with a common denominator and perform the addition.
2. Scheduling Problems:
LCM is essential in scheduling tasks that repeat at different intervals. For instance, if three machines perform maintenance cycles every 3, 6, and 10 days, respectively, the LCM (30) determines when all machines will require maintenance simultaneously.
3. Gear Ratios and Rotational Mechanics:
In mechanical engineering, LCM helps in calculating gear ratios and understanding when different gears will align perfectly, influencing the system's efficiency and synchronization.
4. Music Theory:
LCM plays a role in music theory when dealing with rhythmic patterns and finding the least common multiple of note durations.
5. Data Synchronization and Networking:
In computer networks and data synchronization, LCM helps in determining when different processes or systems will align, optimizing data transfer and preventing conflicts.
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental mathematical skill with widespread applications. While listing multiples works for simple cases, prime factorization offers a more efficient and robust method for calculating LCMs, especially for larger numbers. Understanding the relationship between LCM and GCD provides yet another powerful approach. Mastering LCM calculations enhances problem-solving capabilities in diverse fields, demonstrating the practical relevance of this seemingly basic concept. Remember, the key is to choose the most suitable method depending on the context and the complexity of the numbers involved. Whether you're simplifying fractions, scheduling tasks, or dealing with more complex engineering problems, a thorough understanding of LCM is an invaluable tool.
Latest Posts
Latest Posts
-
Carve Your Name On Your Heart And Not On Marble
May 12, 2025
-
How Many Ounces Is 2 Pounds 7 Ounces Of Butter
May 12, 2025
-
How Long Is Velveeta Good For After Expiration Date
May 12, 2025
-
Who Accepts Wells Fargo Home Projects Card
May 12, 2025
-
What Does It Mean When Someone Calls You A Doll
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 6 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.