What Is The Lcm Of 4 And 15
Arias News
May 11, 2025 · 5 min read
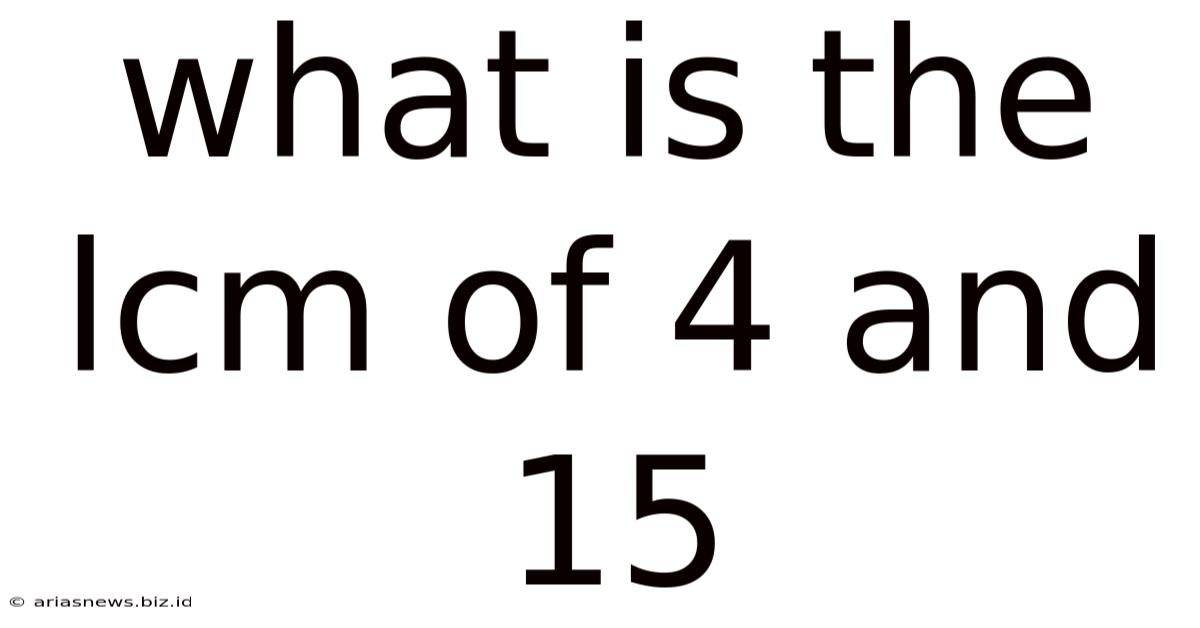
Table of Contents
What is the LCM of 4 and 15? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even music theory. This article will thoroughly explore how to determine the LCM of 4 and 15, and, more importantly, will delve into the underlying principles and various methods for calculating LCMs, equipping you with a comprehensive understanding of this mathematical operation.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 4 and 15, let's establish a solid foundation. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... Multiples of 3 are 3, 6, 9, 12, 15, 18... The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
One straightforward approach to finding the LCM is by listing the multiples of each number until you find the smallest common multiple. Let's apply this method to find the LCM of 4 and 15.
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60...
Multiples of 15: 15, 30, 45, 60, 75, 90...
By comparing the lists, we can see that the smallest number that appears in both lists is 60. Therefore, the LCM of 4 and 15 is 60.
This method works well for smaller numbers but can become cumbersome and time-consuming when dealing with larger numbers. It's important to be methodical and patient when using this approach to avoid missing the LCM.
Method 2: Prime Factorization
A more efficient and systematic method for finding the LCM involves prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Let's find the prime factorization of 4 and 15:
- 4: 2 x 2 = 2²
- 15: 3 x 5
To find the LCM using prime factorization, we follow these steps:
- Identify the prime factors of each number: We've already done this: 2², 3, and 5.
- Find the highest power of each prime factor present in the factorizations: The highest power of 2 is 2², the highest power of 3 is 3¹, and the highest power of 5 is 5¹.
- Multiply the highest powers together: 2² x 3 x 5 = 4 x 3 x 5 = 60
Therefore, the LCM of 4 and 15, using prime factorization, is 60. This method is generally preferred for larger numbers because it's more efficient and less prone to errors.
Method 3: Using the Formula (LCM and GCD Relationship)
The LCM and the greatest common divisor (GCD) of two numbers are intimately related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
To use this method, we first need to find the GCD of 4 and 15. The GCD is the largest number that divides both 4 and 15 without leaving a remainder. In this case, the only common divisor of 4 and 15 is 1. Therefore, GCD(4, 15) = 1.
Now, we can use the formula:
LCM(4, 15) x GCD(4, 15) = 4 x 15
LCM(4, 15) x 1 = 60
LCM(4, 15) = 60
This method elegantly connects the concepts of LCM and GCD, providing another efficient way to calculate the LCM, especially when the GCD is easily determined.
Applications of LCM
The LCM has numerous applications across various fields:
-
Fractions: Finding the LCM is essential when adding or subtracting fractions with different denominators. The LCM of the denominators becomes the common denominator, allowing for straightforward addition or subtraction. For instance, to add 1/4 and 1/15, we'd use the LCM (60) to find the common denominator.
-
Scheduling: The LCM is crucial in scheduling problems, such as determining when two cyclical events will coincide. For example, if two buses arrive at a stop every 4 minutes and 15 minutes respectively, the LCM (60 minutes or 1 hour) indicates when they will both arrive at the stop simultaneously.
-
Music Theory: The LCM helps in understanding musical rhythms and finding the least common period of repeating musical patterns.
-
Modular Arithmetic: LCM plays a critical role in solving problems involving modular arithmetic, which is a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus).
Extending to More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you would simply include all the prime factors of each number and select the highest power of each. For the listing method, the process becomes more complex, requiring more extensive listing and comparison.
Conclusion: Mastering LCM Calculations
This comprehensive guide has explored various methods for calculating the least common multiple, specifically focusing on the LCM of 4 and 15. We've demonstrated that the LCM of 4 and 15 is 60 using three different approaches: listing multiples, prime factorization, and the LCM-GCD relationship formula. Understanding these methods empowers you to tackle LCM problems efficiently and confidently, regardless of the complexity. Remember to choose the method most suitable for the numbers you're working with, prioritizing efficiency and accuracy. The understanding of LCM is a fundamental building block in many mathematical and real-world applications, so mastering its calculation is a valuable skill.
Latest Posts
Latest Posts
-
Can You Freeze Jack Daniels Pulled Pork
May 12, 2025
-
The Amount Of Space An Object Takes Up Is Called
May 12, 2025
-
What Is A Group Of Clams Called
May 12, 2025
-
How Long Will A Skunk Live Without Food Or Water
May 12, 2025
-
Which Statement Is The Best Example Of Rejecting Traditional Beliefs
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 4 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.