What Is The Lcm Of 45 And 30
Arias News
May 12, 2025 · 5 min read
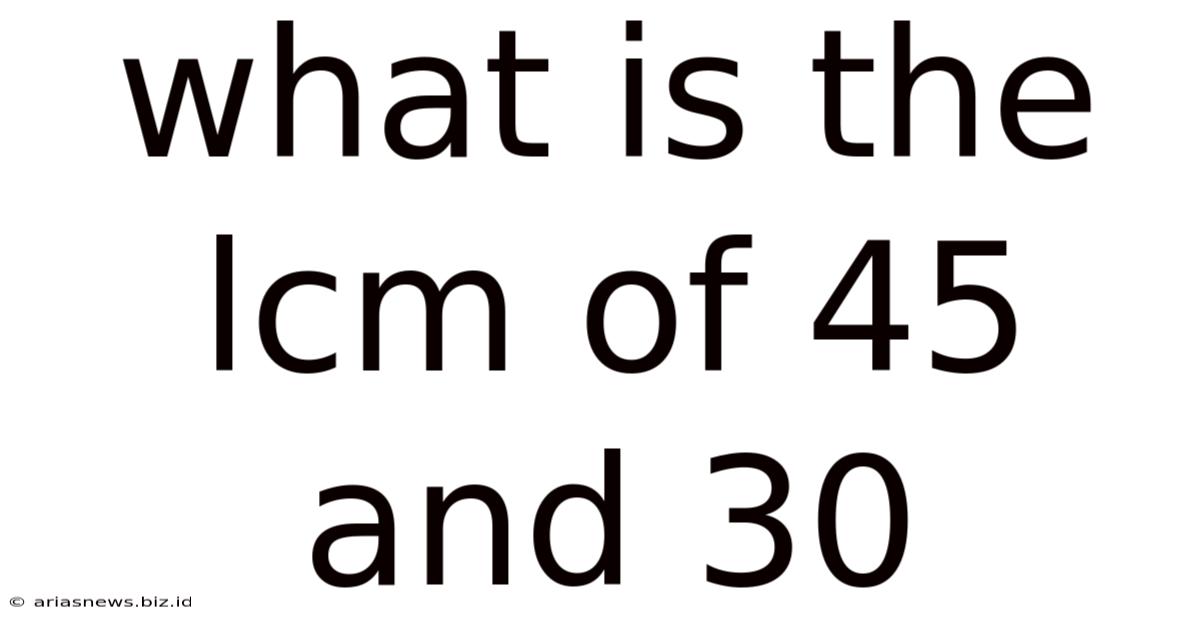
Table of Contents
What is the LCM of 45 and 30? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods to solve it can reveal a wealth of mathematical knowledge. This article will delve deep into the question: What is the LCM of 45 and 30? We'll not only find the answer but also explore various approaches, explaining the rationale behind each method and highlighting their practical applications. We'll also touch upon the broader significance of LCMs in mathematics and beyond.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 45 and 30, let's establish a firm understanding of what an LCM actually is. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... Multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 45 and 30
Several methods can be employed to determine the LCM of 45 and 30. We will explore three common and effective techniques:
1. Listing Multiples
This is the most straightforward method, especially for smaller numbers. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 30: 30, 60, 90, 120, 150, 180...
- Multiples of 45: 45, 90, 135, 180, 225...
Notice that 90 appears in both lists. However, a smaller common multiple, 90, appears first. Therefore, the LCM of 45 and 30 is 90. This method works well for smaller numbers but becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors.
- Prime factorization of 30: 2 x 3 x 5
- Prime factorization of 45: 3 x 3 x 5 = 3² x 5
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(30, 45) = 2 x 3² x 5 = 2 x 9 x 5 = 90
Therefore, the LCM of 45 and 30 is 90 using the prime factorization method. This method is generally preferred for its efficiency and elegance, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula connecting the LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 45 and 30. We can use the Euclidean algorithm for this:
- 45 = 1 x 30 + 15
- 30 = 2 x 15 + 0
The GCD is the last non-zero remainder, which is 15.
Now, we can use the formula:
LCM(45, 30) = (45 x 30) / GCD(45, 30) = (45 x 30) / 15 = 90
Therefore, the LCM of 45 and 30 is 90 using the GCD method. This method is particularly useful when dealing with larger numbers where prime factorization might become cumbersome.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond the realm of abstract mathematics. It finds practical applications in various fields:
-
Scheduling: Imagine you have two machines that complete a cycle in 30 minutes and 45 minutes respectively. To find the time when both machines will complete a cycle simultaneously, you need to find the LCM of 30 and 45, which is 90 minutes.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps you find the least common denominator (LCD), simplifying the calculation.
-
Project Management: In project scheduling, LCM can help determine when different tasks or phases will align, facilitating better coordination and resource allocation.
-
Music Theory: LCM plays a role in determining when rhythms and melodies will synchronize in music composition.
-
Engineering: In various engineering disciplines, LCM is used to calculate periodic events, such as the synchronization of rotating components.
Expanding the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply include all prime factors from all the numbers, taking the highest power of each. For the GCD method, you can iteratively apply the formula, finding the LCM of two numbers at a time.
Conclusion: The Significance of Understanding LCM
The seemingly simple question, "What is the LCM of 45 and 30?" opens the door to a deeper understanding of fundamental mathematical concepts. Mastering the calculation of LCM, through various methods, empowers you to solve a range of real-world problems across diverse fields. The ability to efficiently calculate LCM is a valuable skill, highlighting the importance of understanding not just the answer but the underlying mathematical principles and their practical applications. The ability to utilize different methods demonstrates a versatility and deeper comprehension of the subject matter, making you more adept at tackling more complex mathematical challenges in the future. The exploration of LCM is far more than a simple arithmetic exercise; it’s a stepping stone towards a more profound appreciation of mathematical thinking and its practical relevance.
Latest Posts
Latest Posts
-
How To Address A Letter To A Nursing Home Resident
May 12, 2025
-
Can Bearded Dragons Eat Brussel Sprout Leaves
May 12, 2025
-
How Many Right Angles Does Trapezoid Have
May 12, 2025
-
Kohler 52 50 02 S Cross Reference
May 12, 2025
-
How Much Is 1 Acre Of Land In Mexico
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 45 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.