What Is The Least Common Multiple Of 9 And 10
Arias News
May 10, 2025 · 5 min read
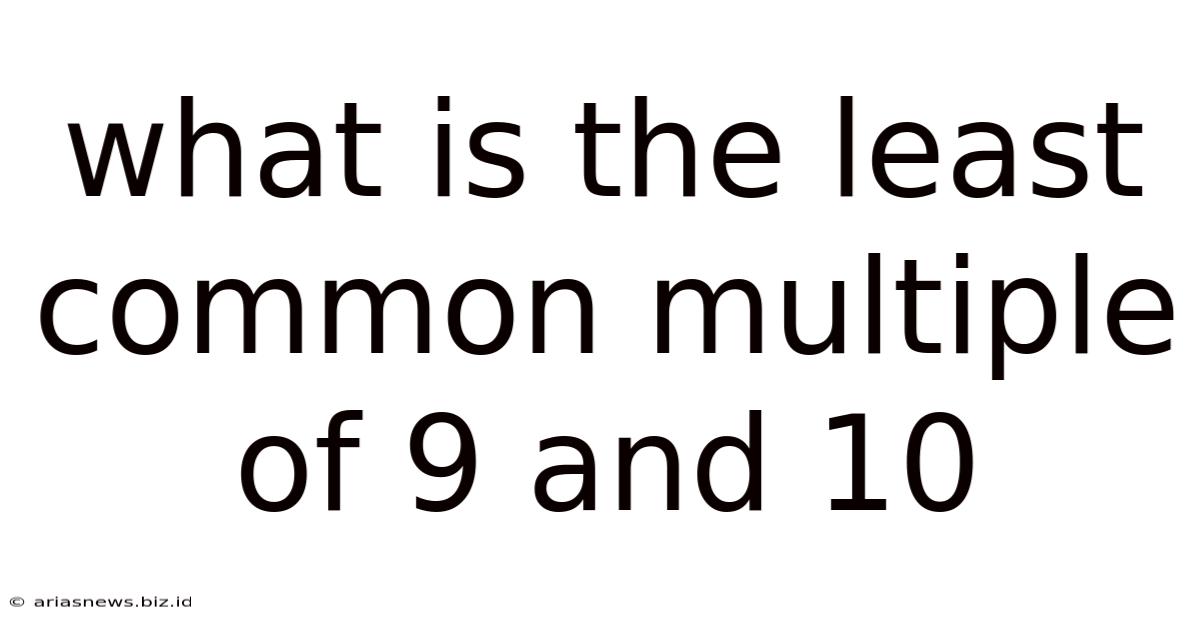
Table of Contents
What is the Least Common Multiple (LCM) of 9 and 10? A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts reveals a fascinating glimpse into number theory. This article explores the LCM of 9 and 10, delving into multiple methods for calculating it and expanding on the broader significance of LCMs in mathematics and real-world applications.
Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. This concept is fundamental in various mathematical fields, including algebra, number theory, and even cryptography.
Why is finding the LCM important?
The LCM finds applications in diverse areas:
- Fractions: Finding a common denominator when adding or subtracting fractions. This ensures a smooth and accurate operation.
- Scheduling: Determining when events with different periodicities will coincide. For example, figuring out when two machines operating at different intervals will require simultaneous maintenance.
- Modular Arithmetic: Used extensively in cryptography and computer science for tasks like encryption and decryption.
- Geometry: In geometric problems involving lengths and areas, finding the LCM can be crucial for calculating sizes and relationships.
Calculating the LCM of 9 and 10: Method 1 - Prime Factorization
The most common and often preferred method to find the LCM involves prime factorization. This method breaks down each number into its prime factors, revealing the building blocks of the number.
Step 1: Prime Factorization of 9
9 can be factored as 3 x 3, or 3².
Step 2: Prime Factorization of 10
10 can be factored as 2 x 5.
Step 3: Identifying Common and Unique Prime Factors
Comparing the prime factorizations, we see that 9 has two factors of 3 and 10 has a factor of 2 and 5. There are no common prime factors between 9 and 10.
Step 4: Calculating the LCM
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together. In this case:
LCM(9, 10) = 2 x 3² x 5 = 2 x 9 x 5 = 90
Therefore, the least common multiple of 9 and 10 is 90.
Calculating the LCM of 9 and 10: Method 2 - Listing Multiples
This method is more intuitive for smaller numbers, though it becomes less efficient for larger ones.
Step 1: Listing Multiples of 9
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, ...
Step 2: Listing Multiples of 10
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
Step 3: Identifying the Least Common Multiple
By comparing the lists, we find that the smallest multiple common to both lists is 90. This confirms our result from the prime factorization method.
Calculating the LCM of 9 and 10: Method 3 - Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are intimately related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers themselves.
Step 1: Finding the GCD of 9 and 10
The GCD is the largest number that divides both 9 and 10 without leaving a remainder. In this case, the GCD(9, 10) = 1, as 1 is the only common divisor.
Step 2: Applying the Formula
The formula relating LCM and GCD is:
LCM(a, b) = (a x b) / GCD(a, b)
Substituting the values:
LCM(9, 10) = (9 x 10) / 1 = 90
Again, this method confirms that the LCM of 9 and 10 is 90.
Beyond the Basics: Extending LCM to More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply consider all the prime factors from all the numbers and take the highest power of each. The listing multiples method becomes increasingly cumbersome with more numbers. The GCD-based method requires a more sophisticated approach using iterative GCD calculations.
Real-world applications of LCM beyond simple calculations
The seemingly simple concept of LCM has far-reaching implications in several real-world scenarios. Here are a few examples:
-
Manufacturing: Imagine a factory producing two different products on separate assembly lines. One line produces a product every 9 minutes, while the other produces a product every 10 minutes. Using the LCM (90 minutes), the factory manager can schedule maintenance or breaks for both lines to coincide, minimizing downtime.
-
Construction: In construction projects, materials might be delivered at different intervals. Determining the LCM of these intervals helps optimize the scheduling of materials handling and storage, ensuring a smooth workflow.
-
Music Theory: In music, the LCM is useful in determining the least common denominator of rhythmic patterns, ensuring that musical phrases align correctly.
-
Scheduling Public Transportation: LCM helps in creating efficient public transportation schedules by identifying the smallest interval at which different bus routes or train lines coincide at a particular stop.
Conclusion: The Power of the LCM
The calculation of the least common multiple of 9 and 10, while seemingly basic, illustrates powerful concepts in number theory and highlights the practical utility of this fundamental mathematical concept. Whether using prime factorization, listing multiples, or the GCD method, understanding the LCM provides a valuable tool for solving problems across various disciplines. Its application extends far beyond simple arithmetic, revealing its importance in optimization, scheduling, and other fields. Mastering the LCM is not just about finding a number; it's about understanding the structure of numbers and their relationships, leading to a deeper appreciation of mathematics and its power in the real world.
Latest Posts
Latest Posts
-
How Many Ounces In Pound Of Gold
May 10, 2025
-
How To Dilute 30 Volume Developer To 20
May 10, 2025
-
4 Oz Of Bacon Is How Many Slices
May 10, 2025
-
What Does Unless Mean In The Lorax
May 10, 2025
-
What Is The Greatest Common Factor Of 34 And 51
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 9 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.