What Is The Midpoint Of The Segment Shown Below
Arias News
Apr 02, 2025 · 6 min read
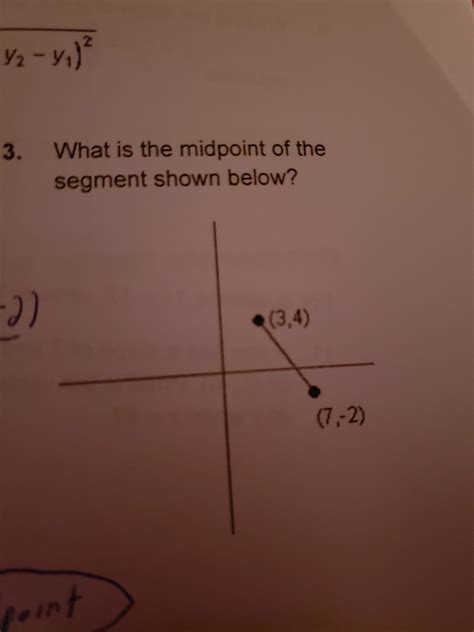
Table of Contents
Decoding the Midpoint: A Comprehensive Guide to Finding the Middle Ground
Finding the midpoint of a line segment is a fundamental concept in geometry with applications extending far beyond the classroom. Whether you're a student tackling geometry problems, a programmer working with coordinate systems, or simply curious about the mathematical elegance of finding the middle ground, this article will provide a comprehensive understanding of midpoint calculation, its variations, and its practical uses.
We'll explore various approaches to determining the midpoint, focusing on the most common methods and providing clear, step-by-step instructions along with numerous examples. By the end of this article, you’ll possess a strong grasp of midpoints and their significance in various fields.
Understanding Line Segments and Midpoints
Before diving into the calculations, let's establish a clear understanding of the terminology. A line segment is a part of a line that is bounded by two distinct endpoints. These endpoints define the length and position of the segment in space.
The midpoint, as the name suggests, is the point that divides the line segment into two equal halves. This point is equidistant from both endpoints. Imagine folding a piece of paper along the line segment—the crease would perfectly bisect the segment, and the point where the crease touches the segment is the midpoint.
Calculating the Midpoint in One Dimension (Number Line)
The simplest scenario involves a line segment on a number line. Let's say we have a segment with endpoints x₁ and x₂. The midpoint, xₘ, is simply the average of the two endpoints:
xₘ = (x₁ + x₂)/2
Example:
Find the midpoint of the line segment with endpoints 2 and 8 on the number line.
- Identify the endpoints: x₁ = 2, x₂ = 8
- Apply the formula: xₘ = (2 + 8)/2 = 10/2 = 5
- Result: The midpoint is 5.
Calculating the Midpoint in Two Dimensions (Coordinate Plane)
The concept extends to two dimensions, where the endpoints are represented by coordinates (x₁, y₁) and (x₂, y₂). To find the midpoint (xₘ, yₘ), we calculate the average of the x-coordinates and the average of the y-coordinates separately:
xₘ = (x₁ + x₂)/2 yₘ = (y₁ + y₂)/2
Example:
Find the midpoint of the line segment with endpoints A(3, 1) and B(7, 5).
- Identify the coordinates: (x₁, y₁) = (3, 1), (x₂, y₂) = (7, 5)
- Calculate the x-coordinate of the midpoint: xₘ = (3 + 7)/2 = 10/2 = 5
- Calculate the y-coordinate of the midpoint: yₘ = (1 + 5)/2 = 6/2 = 3
- Result: The midpoint is (5, 3).
Calculating the Midpoint in Three Dimensions (3D Space)
The principle remains consistent even when we move into three-dimensional space. With endpoints (x₁, y₁, z₁) and (x₂, y₂, z₂), the midpoint (xₘ, yₘ, zₘ) is:
xₘ = (x₁ + x₂)/2 yₘ = (y₁ + y₂)/2 zₘ = (z₁ + z₂)/2
Example:
Find the midpoint of the line segment with endpoints A(1, 2, 3) and B(5, 6, 7).
- Identify the coordinates: (x₁, y₁, z₁) = (1, 2, 3), (x₂, y₂, z₂) = (5, 6, 7)
- Calculate xₘ: xₘ = (1 + 5)/2 = 3
- Calculate yₘ: yₘ = (2 + 6)/2 = 4
- Calculate zₘ: zₘ = (3 + 7)/2 = 5
- Result: The midpoint is (3, 4, 5).
Applications of Midpoint Calculations
The calculation of midpoints is not merely an academic exercise; it has practical applications in diverse fields:
-
Computer Graphics: Midpoint calculations are crucial in computer graphics for tasks such as drawing lines, creating smooth curves (using algorithms like Bresenham's line algorithm which relies on midpoint calculations), and rendering 3D models. Determining the midpoint is vital for efficiently representing and manipulating objects on the screen.
-
Mapping and Navigation: GPS systems and mapping applications rely heavily on coordinate systems. Finding midpoints helps determine central locations, calculate distances, and optimize routes. For instance, the midpoint between two locations can represent a meeting point or the center of a search area.
-
Physics and Engineering: In physics and engineering, calculating the center of mass or centroid of an object often involves finding the midpoint of various line segments or points. This has applications in structural analysis, robotics, and many other fields.
-
Data Analysis and Statistics: Finding the average (mean) of a dataset can be visualized geometrically as finding the midpoint of a line segment representing the minimum and maximum values.
-
Game Development: In game development, the midpoint is frequently used in collision detection, pathfinding algorithms, and other processes that require determining the center of an object or the distance between objects.
Advanced Concepts and Variations
While the basic midpoint formula is straightforward, there are more nuanced situations to consider:
-
Midpoint of a Curve: Finding the midpoint of a curved line segment is more complex and often involves calculus. It requires understanding the equation of the curve and employing techniques like integration or numerical methods.
-
Midpoint in Non-Euclidean Geometry: In non-Euclidean geometries, such as spherical geometry (used in map projections and navigation), the concept of the midpoint is adapted to the specific curvature of the space.
-
Weighted Midpoints: In certain applications, the endpoints might have different weights or importance. In these cases, a weighted average is used to calculate a weighted midpoint. This is common in situations involving center of mass calculations where different parts of the object have different densities.
Troubleshooting Common Mistakes
Here are a few common mistakes to avoid when calculating midpoints:
-
Incorrect Formula: Double-check that you are using the correct formula for the number of dimensions involved (one, two, or three).
-
Incorrect Sign: Be careful with the signs of the coordinates, especially when dealing with negative values.
-
Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) correctly. Parentheses should be calculated first.
-
Unit Consistency: Make sure that the units of measurement are consistent across all coordinates.
Conclusion: Mastering Midpoint Calculations
This comprehensive guide provides a thorough understanding of midpoint calculation across different dimensions and situations. From its fundamental application on a number line to its more complex roles in computer graphics and beyond, mastering midpoint calculations opens up a world of opportunities for tackling diverse problems in mathematics, computer science, engineering, and other quantitative fields. Remember, consistent practice and careful attention to detail will greatly enhance your skill in applying this essential geometrical concept. By understanding the principles and avoiding common pitfalls outlined here, you are well-equipped to confidently tackle any midpoint challenge that may arise.
Latest Posts
Latest Posts
-
Born In 1960 How Old Am I
Apr 03, 2025
-
How Many Ounces In A Kilo Of Coke
Apr 03, 2025
-
How Much Can I Sell A Ps2 For
Apr 03, 2025
-
If You Are 30 What Year Are You Born
Apr 03, 2025
-
Why Is It Called Tossing A Salad
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Midpoint Of The Segment Shown Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
