What Is The Scale Factor From Abc To Def
Arias News
Mar 28, 2025 · 5 min read
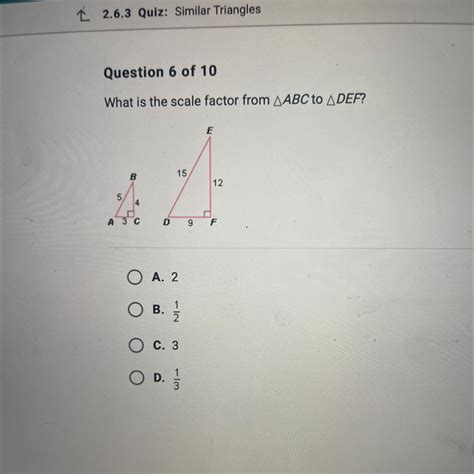
Table of Contents
What is the Scale Factor from ABC to DEF? A Comprehensive Guide
Understanding scale factors is crucial in geometry, particularly when dealing with similar figures. This comprehensive guide will delve deep into determining the scale factor when comparing two similar figures, specifically triangles ABC and DEF. We'll explore various methods, address potential challenges, and provide practical examples to solidify your understanding. By the end, you'll be confidently calculating scale factors between similar shapes.
Understanding Similar Figures and Scale Factors
Before diving into the specifics of triangles ABC and DEF, let's establish a solid foundation. Similar figures are shapes that have the same shape but different sizes. This means their corresponding angles are congruent (equal), and their corresponding sides are proportional. This proportionality is represented by the scale factor.
The scale factor is the ratio of corresponding side lengths between two similar figures. It represents how much larger or smaller one figure is compared to the other. If the scale factor is greater than 1, the second figure is an enlargement of the first. If it's less than 1, the second figure is a reduction of the first.
Determining the Scale Factor from ABC to DEF: A Step-by-Step Approach
Let's assume we have two similar triangles, ABC and DEF. To find the scale factor from ABC to DEF, we need the lengths of corresponding sides. Let's denote the side lengths as follows:
- Triangle ABC: AB, BC, CA
- Triangle DEF: DE, EF, FD
The scale factor (k) from ABC to DEF is calculated using the ratio of corresponding sides:
k = DE/AB = EF/BC = FD/CA
Important Note: The ratio must be consistent for all corresponding sides. If the ratios differ, the triangles are not similar.
Method 1: Using Corresponding Sides
-
Identify Corresponding Sides: Carefully match the corresponding sides of triangles ABC and DEF. This often involves looking at the order of the letters in the triangle names. For instance, side AB corresponds to side DE, BC corresponds to EF, and CA corresponds to FD.
-
Measure Side Lengths: Accurately measure the lengths of corresponding sides of both triangles. You can use a ruler, measuring tape, or any appropriate measuring tool. Ensure you use the same units of measurement for both triangles.
-
Calculate the Ratio: Choose a pair of corresponding sides (e.g., DE and AB). Divide the length of the side in triangle DEF (DE) by the length of the corresponding side in triangle ABC (AB). This will give you the scale factor.
-
Verify with Other Sides: Repeat step 3 for at least one other pair of corresponding sides (e.g., EF and BC, or FD and CA). The ratio should be the same as before. If the ratios are significantly different, double-check your measurements and corresponding side identifications. Inconsistent ratios indicate that the triangles are not similar.
Method 2: Using Given Information
Sometimes, the problem will provide the side lengths directly. In this case, you can skip the measurement step and proceed directly to calculating the ratio. For example, if:
- AB = 4 cm
- BC = 6 cm
- CA = 8 cm
- DE = 6 cm
- EF = 9 cm
- FD = 12 cm
Then the scale factor (k) can be calculated as:
k = DE/AB = 6 cm / 4 cm = 1.5
Verify with another pair:
k = EF/BC = 9 cm / 6 cm = 1.5
k = FD/CA = 12 cm / 8 cm = 1.5
The scale factor from triangle ABC to triangle DEF is 1.5. This means triangle DEF is 1.5 times larger than triangle ABC.
Addressing Potential Challenges and Errors
Several common issues can arise when calculating scale factors. Addressing these proactively ensures accurate results:
-
Incorrect Identification of Corresponding Sides: Double-check the correspondence between sides. Misidentification will lead to an incorrect scale factor. Pay close attention to the order of letters in the triangle names.
-
Measurement Errors: Inaccurate measurements are a significant source of error. Use precise measuring tools and take multiple measurements to minimize errors.
-
Unit Discrepancies: Ensure consistent units throughout the calculation. Mixing units (e.g., centimeters and inches) will lead to an incorrect scale factor.
-
Non-Similar Triangles: If the ratios of corresponding sides are inconsistent, the triangles are not similar, and a single scale factor cannot be determined. Re-examine the given information or your measurements.
Practical Applications and Real-World Examples
Understanding scale factors has widespread applications across numerous fields:
-
Architecture and Engineering: Scale models are essential in designing buildings, bridges, and other structures. The scale factor relates the dimensions of the model to the actual structure.
-
Cartography: Maps are representations of geographical areas, scaled down for convenience. The scale factor indicates the relationship between the map distance and the actual ground distance.
-
Image Processing and Graphics: Enlarging or reducing images involves scaling, and the scale factor defines the level of magnification or reduction.
-
Photography: Understanding scale helps determine the appropriate lens and framing for capturing images.
-
Science and Research: Scale factors are used in microscopy, astronomy, and other scientific fields to represent objects at different magnifications.
Advanced Concepts and Extensions
While we've focused on triangles, the concept of scale factors applies to all similar figures, including quadrilaterals, polygons, and even three-dimensional shapes. The principle remains the same: the ratio of corresponding sides determines the scale factor.
Furthermore, you can use the scale factor to find unknown side lengths in similar figures. If you know the scale factor and the length of one side in one figure, you can calculate the length of the corresponding side in the similar figure.
Conclusion: Mastering Scale Factor Calculations
Calculating the scale factor between two similar figures, like triangles ABC and DEF, involves a systematic approach. By carefully identifying corresponding sides, accurately measuring lengths, and applying the ratio formula, you can confidently determine the scale factor. Remember to verify your results and be mindful of potential sources of error. Mastering scale factor calculations is an essential skill with far-reaching applications in various fields. By understanding the fundamental principles and practical applications discussed in this guide, you'll be well-equipped to tackle scale factor problems with confidence and precision.
Latest Posts
Latest Posts
-
Lowest Common Multiple Of 24 And 30
Mar 31, 2025
-
My Niece Daughter Is What To Me
Mar 31, 2025
-
15 Ml Is Equal To How Many Teaspoons
Mar 31, 2025
-
Four Tenths Of An Hour Is How Many Minutes
Mar 31, 2025
-
How To Make The Paper Fortune Teller
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Scale Factor From Abc To Def . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
