What Is The Shape With 9 Sides Called
Arias News
Apr 04, 2025 · 5 min read
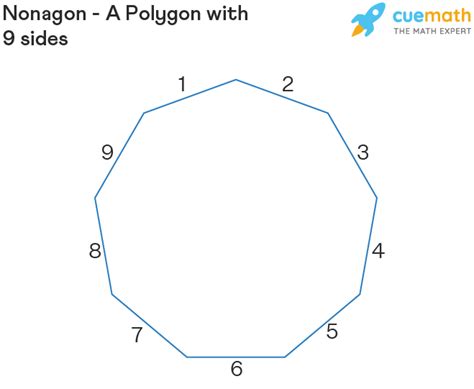
Table of Contents
What is the Shape with 9 Sides Called? A Deep Dive into Nonagons
Have you ever wondered about the name of a shape with nine sides? It's a question that might seem simple at first, but delving into the world of polygons reveals a fascinating journey through geometry, history, and even art. This comprehensive guide will explore the fascinating world of nonagons, explaining their properties, applications, and the rich mathematical context surrounding them.
Understanding Polygons: The Building Blocks of Shapes
Before we dive into the specifics of nine-sided shapes, it's important to establish a foundational understanding of polygons. A polygon is a closed two-dimensional figure formed by connecting a set of straight line segments. These segments are called the sides of the polygon, and the points where the sides meet are called the vertices or angles.
Polygons are classified primarily by the number of sides they have. Some common examples include:
- Triangle (3 sides): The simplest polygon, forming the basis for countless geometric constructions.
- Quadrilateral (4 sides): Encompassing squares, rectangles, trapezoids, and rhombuses, quadrilaterals are ubiquitous in everyday life.
- Pentagon (5 sides): Famous for its appearance in the Pentagon building and in many geometric designs.
- Hexagon (6 sides): Common in nature, notably in honeycombs and certain crystals.
- Heptagon (7 sides): Less common than other polygons but still holds mathematical significance.
- Octagon (8 sides): Often seen in stop signs and architectural designs.
- Nonagon (9 sides): Our focus for this article!
- Decagon (10 sides): And many more beyond!
Introducing the Nonagon: The Shape with Nine Sides
So, what is a shape with nine sides called? The answer is a nonagon. Also known as an enneagon, this polygon holds a unique place in the world of geometry. While not as frequently encountered as triangles, squares, or hexagons, the nonagon possesses intriguing properties and finds applications in various fields.
Properties of a Nonagon
Like all polygons, a nonagon has several key properties:
- Nine Sides and Nine Angles: This is the defining characteristic of a nonagon.
- Interior Angles: The sum of the interior angles of any nonagon is (9-2) * 180° = 1260°. This is a general formula applicable to all polygons.
- Regular Nonagon: A regular nonagon is one where all nine sides are equal in length, and all nine angles are equal (each measuring 140°). This creates a highly symmetrical and aesthetically pleasing shape.
- Irregular Nonagons: Many nonagons are irregular, meaning their sides and angles are of varying lengths and measures.
Constructing a Nonagon
Constructing a regular nonagon using only a compass and straightedge is not possible. This is because 9 is not a Fermat prime. However, it can be approximated using various geometric techniques or with the help of computer-aided design (CAD) software. Approximation methods often involve iterative processes to refine the shape closer to a true regular nonagon.
Nonagons in Art, Design, and Architecture
While not as prevalent as some other polygons, the nonagon makes subtle appearances in various fields:
- Tessellations: While a regular nonagon cannot tessellate (tile a plane without gaps or overlaps), combinations of nonagons with other polygons can create interesting tessellation patterns.
- Islamic Art: The rich symmetry and geometric complexity of Islamic art often incorporates polygons, including nonagons, in intricate designs that decorate mosques, palaces, and other structures. The balance and repetition found in these designs reflect deep mathematical principles.
- Architectural Design: Although less common than other shapes, nonagons might appear in subtle details of building designs, window frames, or decorative elements. The unique shape adds a touch of intrigue and complexity.
- Logos and Branding: The unusual nature of the nonagon can make it a striking choice for logos and branding, creating a memorable and distinct visual identity.
- Computer Graphics and Game Design: Nonagons can be used to create unique shapes and environments in computer-generated imagery and video games, enhancing the visual appeal and diversity of the game world.
Mathematical Exploration of Nonagons
Beyond its visual applications, the nonagon offers fertile ground for mathematical exploration:
- Area Calculation: The area of a regular nonagon can be calculated using the formula: A = (9/4) * s² * cot(π/9), where 's' is the length of a side. This formula showcases the connection between trigonometry and geometry.
- Relationship to Other Polygons: The nonagon's properties are interconnected with those of other polygons, forming part of a broader geometric framework. Exploring these relationships helps deepen understanding.
- Symmetry Groups: The regular nonagon possesses a high degree of rotational and reflectional symmetry, which is a subject of study in group theory.
- Approximations and Constructions: The challenges in constructing a precise regular nonagon with compass and straightedge lead to innovative approximation techniques, fostering mathematical creativity.
Beyond the Basics: Deeper Mathematical Concepts
The nonagon, while seemingly a simple shape, connects to deeper mathematical concepts:
- Trigonometry: The calculation of the area and other properties of a nonagon relies heavily on trigonometric functions, particularly concerning angles and side lengths. Understanding these trigonometric relationships is crucial for comprehending nonagonal geometry.
- Complex Numbers: Complex numbers can be used to represent the vertices of a regular nonagon in the complex plane, allowing for elegant mathematical manipulation and analysis of the shape's properties.
- Abstract Algebra: The symmetries of a regular nonagon are studied within abstract algebra, providing a rich mathematical context that extends beyond basic geometry.
- Topology: Topology, the study of shapes and spaces under continuous transformations, offers a different perspective on the nonagon, focusing on its overall structure and connectivity rather than precise measurements.
Conclusion: The Enduring Fascination of the Nonagon
The seemingly simple question, "What is the shape with 9 sides called?" opens a door to a fascinating exploration of geometry, art, and mathematics. The nonagon, though less common than other polygons, holds a unique place in the mathematical landscape. Its properties, its applications in design, and its connection to deeper mathematical concepts reveal the rich tapestry of knowledge woven into this nine-sided shape. From its subtle presence in architectural details to its more prominent role in mathematical exploration, the nonagon continues to fascinate and inspire. Understanding its properties and applications enhances our appreciation for the beauty and complexity of the mathematical world.
Latest Posts
Latest Posts
-
How Many Cups Is 238 Grams Of Powder
Apr 05, 2025
-
How Much Does A 5 Gallon Bucket Of Corn Weigh
Apr 05, 2025
-
What Does Hr Stand For In Person Of Interest
Apr 05, 2025
-
How Much Is 2 3 Plus 2 3
Apr 05, 2025
-
1 Square Foot Is How Many Square Inches
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Shape With 9 Sides Called . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
