What Is The Unit Value Of The 6 In 216
Arias News
May 08, 2025 · 5 min read
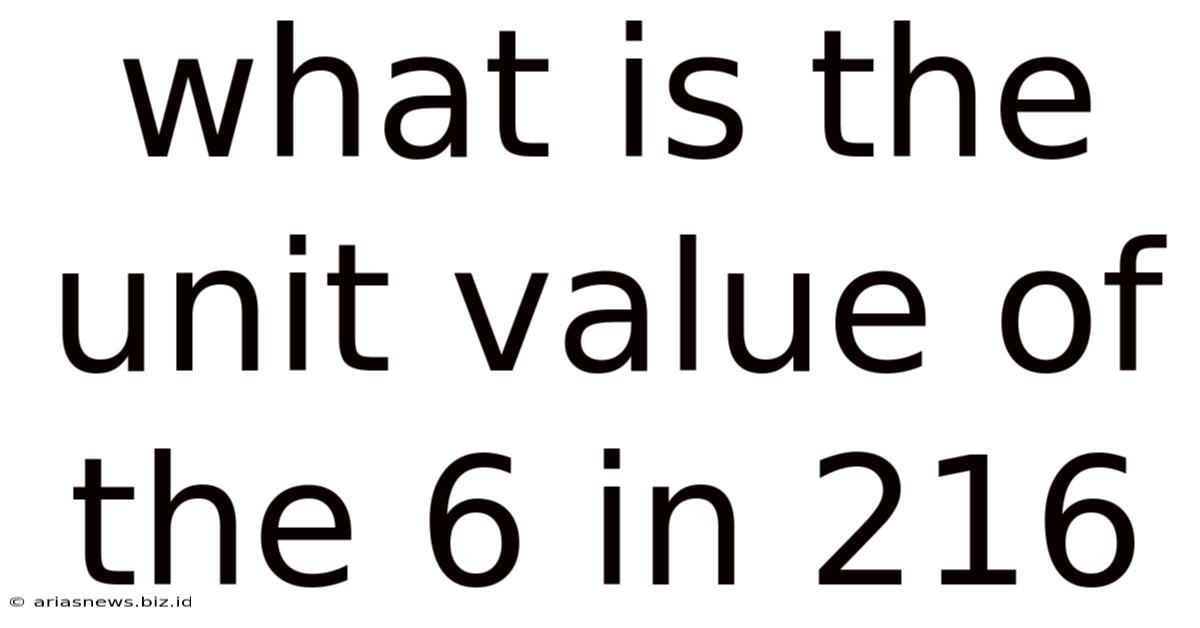
Table of Contents
What is the Unit Value of the 6 in 216? A Deep Dive into Place Value
Understanding place value is fundamental to comprehending mathematics, particularly when working with larger numbers. This article delves into the concept of place value, specifically addressing the question: What is the unit value of the 6 in 216? We'll explore this seemingly simple question in detail, examining the underlying principles and expanding upon related concepts to provide a comprehensive understanding.
Understanding Place Value: The Foundation of Numerical Representation
Before we pinpoint the unit value of the 6 in 216, let's establish a strong foundation in place value. Our number system is a base-10 system, also known as the decimal system. This means it's based on powers of 10. Each digit in a number holds a specific place, and its value depends on its position within the number.
The Power of Ten: A Hierarchical System
Consider the number 216. We can break it down as follows:
- 2 (hundreds place): This 2 represents 2 x 100 = 200. It's in the hundreds place, representing two sets of one hundred.
- 1 (tens place): This 1 represents 1 x 10 = 10. It's in the tens place, representing one set of ten.
- 6 (ones place or units place): This 6 represents 6 x 1 = 6. It's in the ones (or units) place, representing six individual units.
This hierarchical structure allows us to represent large numbers using only ten digits (0-9). Each position represents a progressively higher power of 10, moving from right to left.
Determining the Unit Value of the 6 in 216
Now, we can directly answer the initial question: What is the unit value of the 6 in 216?
The unit value of a digit simply refers to its value as a single unit. In the number 216, the 6 is in the ones (or units) place. Therefore, the unit value of the 6 in 216 is 6. It represents six individual units, and its value is simply 6.
Distinguishing Unit Value from Place Value
It's crucial to distinguish between unit value and place value. The unit value is the inherent value of the digit itself (in this case, 6). The place value signifies the positional value of the digit within the number, indicating the power of 10 it represents (in this case, 1, since it's in the ones place).
Expanding on Place Value: Exploring Larger Numbers
The principles of place value extend far beyond the hundreds place. Let's consider a larger number, such as 12,345,678.
- 8 (ones/units): Unit value = 8, Place value = 1
- 7 (tens): Unit value = 7, Place value = 10
- 6 (hundreds): Unit value = 6, Place value = 100
- 5 (thousands): Unit value = 5, Place value = 1000
- 4 (ten thousands): Unit value = 4, Place value = 10,000
- 3 (hundred thousands): Unit value = 3, Place value = 100,000
- 2 (millions): Unit value = 2, Place value = 1,000,000
- 1 (ten millions): Unit value = 1, Place value = 10,000,000
As you can see, the unit value remains consistent, while the place value increases exponentially with each position shift to the left.
Applications of Place Value in Daily Life
Understanding place value isn't just an academic exercise; it's crucial for everyday life. We use it constantly, often without realizing it:
- Money: When working with currency, understanding place value is essential for accurate calculations. For example, $123.45 involves the place values of ones, tens, hundreds, tenths, and hundredths.
- Measurements: Measurements of length (meters, centimeters), weight (kilograms, grams), and volume (liters, milliliters) rely heavily on place value.
- Data Analysis: Interpreting data presented in charts and graphs often requires understanding the place values represented.
- Programming: In computer science, understanding the representation of numbers in binary (base-2) or other bases relies on similar principles of place value.
Beyond Base-10: Exploring Other Number Systems
While our daily lives primarily utilize the base-10 system, other number systems exist. These systems follow the same fundamental principles of place value but use different bases. For example:
- Binary (Base-2): Uses only two digits (0 and 1). Common in computer science.
- Hexadecimal (Base-16): Uses sixteen digits (0-9 and A-F). Often used in color codes and memory addresses.
Understanding place value is key to understanding any number system, regardless of its base. The fundamental concept remains consistent: each digit's value depends on its position within the number.
Common Mistakes and Misconceptions
Even though the concept of place value seems straightforward, several common misconceptions can arise:
- Confusing Unit Value and Place Value: As mentioned earlier, it's crucial to distinguish between the inherent value of the digit (unit value) and the value derived from its position (place value).
- Difficulty with Larger Numbers: Working with very large numbers can sometimes cause confusion regarding the appropriate place values. Breaking down the number into smaller components can help.
- Ignoring Leading Zeros: Leading zeros (e.g., 0025) do not change the value of the number. They simply indicate the number of places the digits occupy.
Practice Problems and Exercises
To solidify your understanding of place value, try the following exercises:
- What is the unit value of the 7 in 7,432?
- What is the place value of the 5 in 15,826?
- What is the unit value of each digit in 9,876,543,210?
- Write the number 3 thousands, 2 hundreds, 5 tens, and 8 ones in standard form.
- Express the number 426 in expanded form (e.g., 200 + 10 + 6).
By practicing these problems, you can strengthen your understanding and apply place value concepts with confidence.
Conclusion: Mastering Place Value for Mathematical Success
This comprehensive exploration of place value, focusing specifically on the unit value of the 6 in 216, underscores its fundamental importance in mathematics and everyday life. Understanding place value is not just about memorizing definitions; it's about grasping the underlying structure of our number system, which empowers you to work confidently with numbers of any size and in various contexts. From financial calculations to data analysis and computer programming, a strong grasp of place value forms a crucial foundation for mathematical success. Continuously practicing and applying these concepts will ensure mastery and pave the way for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
How Many Triangles Are In A Heptagon
May 11, 2025
-
How Much Is 10 Liters In Pounds
May 11, 2025
-
Can You Eat Mushrooms That Grow In Horse Manure
May 11, 2025
-
Is Blue Color A Chemical Or Physical Property
May 11, 2025
-
How Much Is 100 Ounces Of Water In Litres
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Unit Value Of The 6 In 216 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.