What Is The Value Of X In The Rhombus Below
Arias News
Mar 30, 2025 · 6 min read
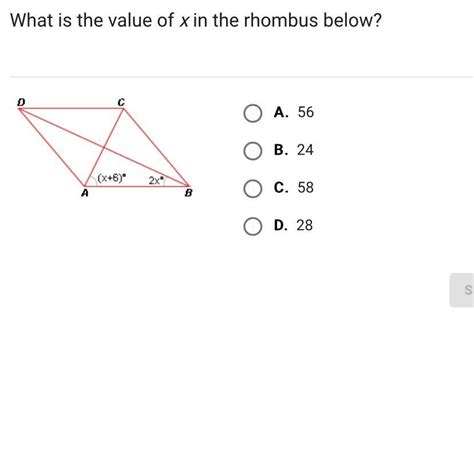
Table of Contents
Unlocking the Mystery: Solving for x in a Rhombus
The seemingly simple question – "What is the value of x in the rhombus below?" – hides a wealth of mathematical concepts. Understanding how to solve for x requires a solid grasp of rhombus properties, algebraic manipulation, and potentially, trigonometric functions depending on the information provided. This comprehensive guide will explore various scenarios and techniques to determine the value of x, focusing on different types of problems and emphasizing the underlying geometric principles.
Before diving into specific examples, let's establish a strong foundation by reviewing the key properties of a rhombus:
Understanding Rhombus Properties: The Foundation of Our Solution
A rhombus is a quadrilateral (a four-sided polygon) with all four sides equal in length. This seemingly simple definition unlocks several crucial properties that are essential for solving for x:
-
Opposite sides are parallel: This property is inherited from the broader parallelogram family to which rhombuses belong. Knowing that opposite sides are parallel allows us to utilize alternate interior angles and corresponding angles theorems.
-
Opposite angles are equal: This means that opposite angles within the rhombus have the same measure. This is incredibly useful when dealing with angles within the problem.
-
Consecutive angles are supplementary: This means that any two angles that share a side add up to 180 degrees. This supplementary angle relationship is another powerful tool for solving problems.
-
Diagonals bisect each other: The diagonals of a rhombus (lines connecting opposite vertices) intersect at a point that divides each diagonal into two equal segments. This bisection creates four congruent right-angled triangles.
-
Diagonals are perpendicular bisectors: This means the diagonals intersect at a 90-degree angle and each diagonal bisects (cuts in half) the other. This property is crucial when applying trigonometric functions or Pythagorean theorem.
Case Study 1: Using Angle Properties to Solve for x
Scenario: Imagine a rhombus where two consecutive angles are given as expressions involving x. For instance, one angle is 2x + 10 degrees, and the adjacent angle is 3x - 20 degrees.
Solution:
Since consecutive angles in a rhombus are supplementary, we can set up an equation:
(2x + 10) + (3x - 20) = 180
Simplifying and solving for x:
5x - 10 = 180 5x = 190 x = 38
Therefore, in this scenario, the value of x is 38.
Case Study 2: Leveraging Opposite Angles and Equations
Scenario: Consider a rhombus where opposite angles are given as expressions of x. Let's say one opposite angle is 4x and the other is x + 45.
Solution:
Because opposite angles in a rhombus are equal, we can set up the equation:
4x = x + 45
Solving for x:
3x = 45 x = 15
In this case, the value of x is 15.
Case Study 3: Introducing the Power of Diagonals
Scenario: A rhombus has diagonals of length 6 and 8. One of the triangles formed by the intersection of the diagonals contains an angle expressed as 2x.
Solution:
The diagonals of a rhombus intersect at right angles, forming four congruent right-angled triangles. We can use trigonometry (specifically, trigonometric ratios like tangent, sine, or cosine) to solve for x.
Let's say the angle 2x is one of the acute angles in the right-angled triangle. Knowing that the legs of the right-angled triangle have lengths 3 (half of the 6 diagonal) and 4 (half of the 8 diagonal), we can use the trigonometric function tan (tangent):
tan(2x) = opposite/adjacent = 4/3
To find x, we need to use the inverse tangent function (arctan or tan⁻¹):
2x = arctan(4/3)
Calculate arctan(4/3) using a calculator, then divide the result by 2 to find x.
Case Study 4: Pythagorean Theorem and Rhombus Side Lengths
Scenario: A rhombus has side length denoted by the expression 2x + 1. The length of one diagonal is given as 10, and the length of the other diagonal is 6.
Solution:
The diagonals of a rhombus divide it into four congruent right-angled triangles. The sides of these triangles are half the lengths of the diagonals and the side of the rhombus.
Using the Pythagorean theorem (a² + b² = c²), where a and b are half the diagonal lengths, and c is the rhombus side length:
(10/2)² + (6/2)² = (2x + 1)²
5² + 3² = (2x + 1)²
25 + 9 = (2x + 1)²
34 = (2x + 1)²
Taking the square root of both sides:
√34 = 2x + 1
Solving for x:
2x = √34 - 1 x = (√34 - 1) / 2
This will give you the exact value of x. You can use a calculator to find an approximate decimal value.
Case Study 5: Advanced Scenarios – Area and Perimeter
Scenario: The area of a rhombus is given as a function of x, and its perimeter is also given as a function of x.
Solution:
The area of a rhombus can be calculated as (1/2)d₁d₂, where d₁ and d₂ are the lengths of the diagonals. The perimeter is simply 4 times the side length.
This scenario requires a system of equations. Using the area formula and the perimeter formula, you'll have two equations involving x. Solve these equations simultaneously to find the value of x.
Case Study 6: Using Coordinate Geometry
Scenario: The vertices of a rhombus are given as coordinates on a Cartesian plane.
Solution:
Coordinate geometry provides a powerful tool to solve for x. You can use the distance formula to find the lengths of the sides (which must be equal). The midpoint formula can be used to verify that the diagonals bisect each other. The slope formula can determine the perpendicularity of diagonals. By using appropriate formulas and setting up equations based on the rhombus properties, you can solve for x.
Mastering Rhombus Problems: Tips and Tricks
-
Draw a diagram: Always start by drawing a clear diagram of the rhombus, labeling all known values and angles. A visual representation will help you identify the relevant properties and relationships.
-
Identify the given information: Carefully examine the problem statement to identify all the given information, such as angles, side lengths, or diagonal lengths.
-
Choose the appropriate method: Select the most appropriate method based on the given information. This might involve using angle relationships, the Pythagorean theorem, trigonometric functions, or a system of equations.
-
Check your work: After solving for x, take the time to check your solution. Substitute the value of x back into the original equations and verify that your solution is consistent with the properties of a rhombus.
-
Practice makes perfect: The best way to master solving for x in rhombus problems is to practice. Work through a variety of problems with different types of given information and techniques.
By understanding the fundamental properties of rhombuses and employing the appropriate mathematical tools, you can confidently solve for x in a wide range of scenarios. Remember to always approach these problems systematically and methodically, and don't be afraid to use a calculator to aid in calculations involving trigonometric functions or square roots. With consistent practice and a solid grasp of geometric principles, you'll become a rhombus-solving master!
Latest Posts
Latest Posts
-
Whats The Front Of A Train Called
Apr 01, 2025
-
How Many Blades Of Grass In The World
Apr 01, 2025
-
What Is 1 Trillionth To The 10th Power
Apr 01, 2025
-
How Many Plutos Can Fit In The Sun
Apr 01, 2025
-
Continuous Hard Braking On Ice And Snow Often
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of X In The Rhombus Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
