What Is The Volume Of The Cylinder Shown Below
Arias News
Mar 31, 2025 · 4 min read
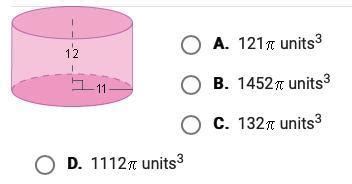
Table of Contents
What is the Volume of the Cylinder Shown Below? A Comprehensive Guide
This article will delve deep into calculating the volume of a cylinder, addressing various scenarios and complexities. We'll explore the fundamental formula, discuss practical applications, and tackle problems that require a more nuanced understanding. We'll also cover related concepts like surface area and how changes in dimensions affect the overall volume. Let's begin!
Understanding the Basics: The Cylinder and its Dimensions
A cylinder is a three-dimensional geometric shape with two parallel circular bases connected by a curved surface. Imagine a can of soup or a pipe – these are perfect examples of cylinders. To calculate its volume, we need two key measurements:
- Radius (r): The distance from the center of the circular base to any point on the edge of the circle.
- Height (h): The perpendicular distance between the two circular bases.
The Fundamental Formula: Calculating the Volume
The formula for calculating the volume (V) of a cylinder is remarkably straightforward:
V = πr²h
Where:
- V represents the volume
- π (pi) is a mathematical constant, approximately equal to 3.14159
- r is the radius of the circular base
- h is the height of the cylinder
This formula essentially calculates the area of the circular base (πr²) and then multiplies it by the height (h) to determine the total volume. Think of it as stacking many identical circles on top of each other to create the cylinder.
Step-by-Step Calculation: A Practical Example
Let's assume we have a cylinder with a radius of 5 cm and a height of 10 cm. Here's how we would calculate its volume:
-
Identify the known values: r = 5 cm, h = 10 cm
-
Substitute the values into the formula: V = π * (5 cm)² * 10 cm
-
Calculate the squared radius: (5 cm)² = 25 cm²
-
Perform the multiplication: V = π * 25 cm² * 10 cm = 250π cm³
-
Use the approximate value of π (3.14159): V ≈ 250 * 3.14159 cm³ ≈ 785.3975 cm³
Therefore, the volume of the cylinder is approximately 785.4 cubic centimeters.
Units of Measurement: Maintaining Consistency
It's crucial to maintain consistency in units of measurement throughout the calculation. If the radius is given in centimeters, the height must also be in centimeters. The resulting volume will then be in cubic centimeters (cm³). If using different units (e.g., inches, meters), ensure consistent application to avoid errors.
Beyond the Basics: Dealing with Complex Scenarios
While the basic formula is relatively simple, certain scenarios might present additional challenges:
1. Oblique Cylinders:
An oblique cylinder has its axis tilted, not perpendicular to its bases. While the formula remains the same (V = πr²h), it's critical to use the perpendicular height (h) – the distance between the two bases measured along a line perpendicular to both bases. The slanted height is not relevant for volume calculation.
2. Cylinders with Unknown Radius:
If the radius is unknown but the diameter (d) is given, remember that the radius is half the diameter: r = d/2. Substitute this value into the volume formula.
3. Cylinders with Complex Shapes:
Some applications may involve cylinders with non-circular bases (e.g., elliptical cylinders). The volume calculation becomes more complex and requires specialized formulas based on the shape of the base.
4. Hollow Cylinders:
For a hollow cylinder (like a pipe), you need to calculate the volume of the outer cylinder and subtract the volume of the inner cylinder. This requires knowing both the inner and outer radii.
Practical Applications of Cylinder Volume Calculations
Understanding cylinder volume calculations is crucial in various fields:
- Engineering: Calculating the capacity of pipes, tanks, and other cylindrical structures.
- Manufacturing: Determining the amount of material needed to create cylindrical components.
- Construction: Estimating the volume of cylindrical columns or supports.
- Science: Measuring the volume of liquids in cylindrical containers.
Related Concepts: Surface Area of a Cylinder
While this article focuses on volume, it's helpful to understand the related concept of surface area. The total surface area (A) of a cylinder consists of the areas of its two circular bases and its curved surface:
A = 2πr² + 2πrh
Knowing both the volume and surface area of a cylinder can be invaluable in various applications, particularly in material science and engineering design.
Advanced Topics and Further Exploration
More complex applications might involve integrating calculus to calculate volumes of irregular cylinders or cylinders with variable radius. These advanced techniques require a deeper understanding of mathematical principles.
Conclusion: Mastering Cylinder Volume Calculation
Calculating the volume of a cylinder is a fundamental skill in various fields. By understanding the basic formula (V = πr²h) and its applications, you can solve a wide range of problems. Remember to pay close attention to units of measurement and consider the specific nuances of complex cylinder shapes or scenarios. This comprehensive guide provides a solid foundation for understanding and applying this important mathematical concept. Through practice and problem-solving, you will gain proficiency in this crucial skill, which has far-reaching implications in numerous practical applications. Continued exploration of related geometric concepts and mathematical principles will further enhance your understanding and ability to tackle more challenging problems in the future. Remember to always double-check your work and utilize various resources to verify your results, ensuring accuracy and a deeper comprehension of the subject matter.
Latest Posts
Latest Posts
-
Foods That Begin With The Letter X
Apr 02, 2025
-
How Many Slices Of Cheese In A Pound
Apr 02, 2025
-
How Many Lbs Of Blueberries In A Gallon
Apr 02, 2025
-
How Long Is 13 Cm In Inches
Apr 02, 2025
-
How Many Cups In A Pound Of Blueberries
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Volume Of The Cylinder Shown Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
