What Percent Is 4 Out Of 16
Arias News
May 10, 2025 · 5 min read
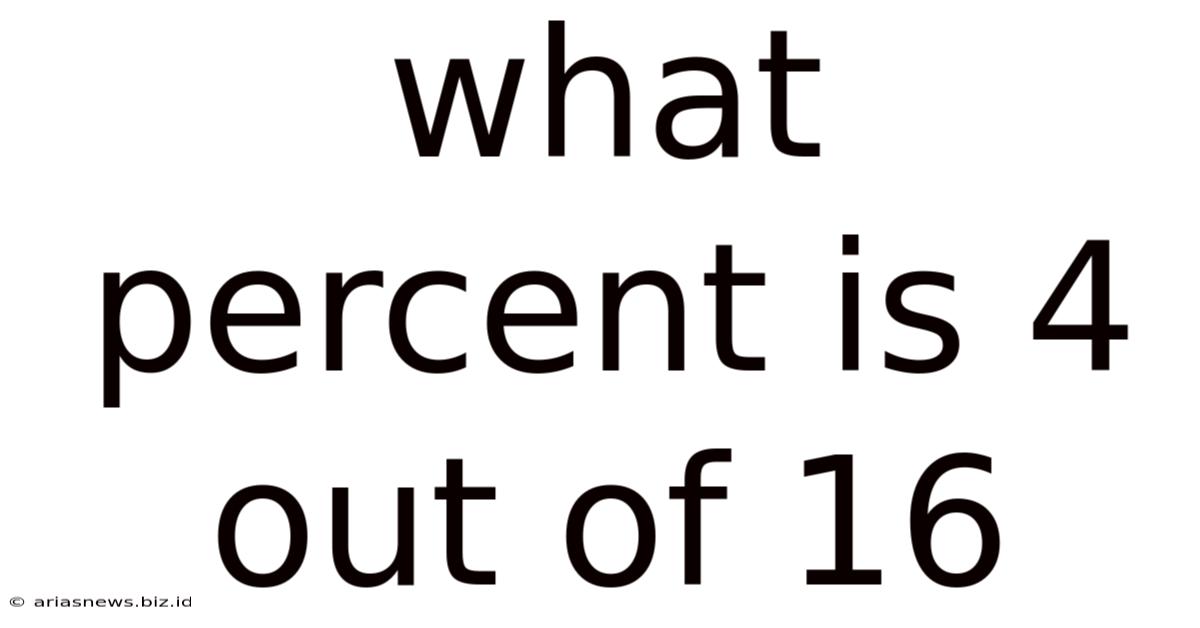
Table of Contents
What Percent is 4 out of 16? A Deep Dive into Percentages and Their Applications
Determining what percent 4 is out of 16 is a fundamental concept in mathematics with wide-ranging applications in various fields. This seemingly simple calculation serves as a gateway to understanding percentages, ratios, fractions, and their practical uses in everyday life and professional settings. This comprehensive guide will not only answer the core question but will also delve into the underlying principles, explore different calculation methods, and showcase real-world examples to solidify your comprehension.
Understanding Percentages: The Building Blocks
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ( per cent). Therefore, 25% means 25 out of 100, which can be expressed as the fraction 25/100 or the decimal 0.25.
Understanding this foundational concept is crucial for tackling percentage problems effectively. Many everyday situations involve percentages, from calculating sales tax and discounts to understanding interest rates and statistical data.
Key Terms and Concepts:
- Fraction: A representation of a part of a whole, expressed as a/b (where 'a' is the numerator and 'b' is the denominator).
- Ratio: A comparison of two quantities, often expressed as a:b or a/b.
- Decimal: A number expressed in base-10, using a decimal point to separate the whole number from the fractional part.
- Proportion: An equation stating that two ratios are equal.
Calculating "What Percent is 4 out of 16?" – Three Methods
There are several ways to calculate what percentage 4 represents out of 16. Let's explore three common methods:
Method 1: Using the Fraction Method
This is perhaps the most intuitive method. We can represent "4 out of 16" as the fraction 4/16. To convert this fraction into a percentage, we need to express it as a fraction with a denominator of 100.
-
Simplify the fraction: 4/16 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 4. This simplifies the fraction to 1/4.
-
Convert to a fraction with a denominator of 100: To convert 1/4 to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by 25: (1 x 25) / (4 x 25) = 25/100.
-
Express as a percentage: Since 25/100 represents 25 out of 100, the answer is 25%.
Method 2: Using the Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100.
-
Convert the fraction to a decimal: Divide the numerator (4) by the denominator (16): 4 ÷ 16 = 0.25
-
Multiply by 100: Multiply the decimal by 100 to convert it to a percentage: 0.25 x 100 = 25
-
Express as a percentage: The answer is 25%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We set up a proportion where x represents the unknown percentage:
4/16 = x/100
To solve for x, we cross-multiply:
16x = 400
Divide both sides by 16:
x = 25
Therefore, the answer is 25%.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world scenarios. Here are a few examples:
1. Sales and Discounts:
Imagine a store offers a 25% discount on a $100 item. To calculate the discount amount, you would multiply the original price by the percentage (100 x 0.25 = $25). The final price would be $75.
2. Interest Rates:
Understanding interest rates is crucial for managing finances. If you deposit $1000 in a savings account with a 5% annual interest rate, you'll earn $50 in interest after one year (1000 x 0.05 = 50).
3. Tax Calculations:
Sales tax is often expressed as a percentage. If the sales tax rate is 8%, you'd calculate the tax amount by multiplying the price of the item by 0.08.
4. Statistics and Data Analysis:
Percentages are frequently used to represent data in various fields, including healthcare, business, and social sciences. For example, a survey might reveal that 60% of respondents prefer a particular product.
5. Grade Calculations:
In education, percentages are used to represent scores and grades. If you answer 15 out of 20 questions correctly on a test, your score is 75% (15/20 x 100 = 75).
Beyond the Basics: Advanced Percentage Applications
The fundamental understanding of percentages extends to more complex calculations and concepts:
1. Percentage Increase and Decrease:
These calculations involve determining the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] x 100. A similar formula applies to percentage decrease.
2. Percentage Points:
It's crucial to differentiate between percentage points and percentages. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase relative to the original value.
3. Compound Interest:
Compound interest calculates interest not only on the principal amount but also on accumulated interest. This results in exponential growth over time.
4. Percentage Yield in Chemistry:
In chemistry, percentage yield represents the efficiency of a chemical reaction. It compares the actual yield to the theoretical yield.
Conclusion: Mastering Percentages for Success
The seemingly simple question, "What percent is 4 out of 16?" opens the door to a vast world of percentage applications. Understanding how to calculate percentages is a crucial skill applicable across various disciplines and everyday scenarios. By mastering the different methods presented in this guide – the fraction method, the decimal method, and the proportions method – you'll be equipped to tackle diverse percentage problems with confidence. Remember the real-world examples and advanced concepts to expand your understanding and apply this knowledge effectively in your personal and professional life. From managing finances to interpreting data, a strong grasp of percentages is a key component of numerical literacy and successful problem-solving.
Latest Posts
Latest Posts
-
The Three Altitudes Of A Triangle Intersect At The
May 10, 2025
-
Te Amo Siempre Y Para Siempre In English
May 10, 2025
-
5 X 10 To The Power Of 3
May 10, 2025
-
What Grade Is A 8 Out Of 10
May 10, 2025
-
Which Side Goes Up On A Winter Pool Cover
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 4 Out Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.