What Percent Is 8 Out Of 24
Arias News
May 10, 2025 · 5 min read
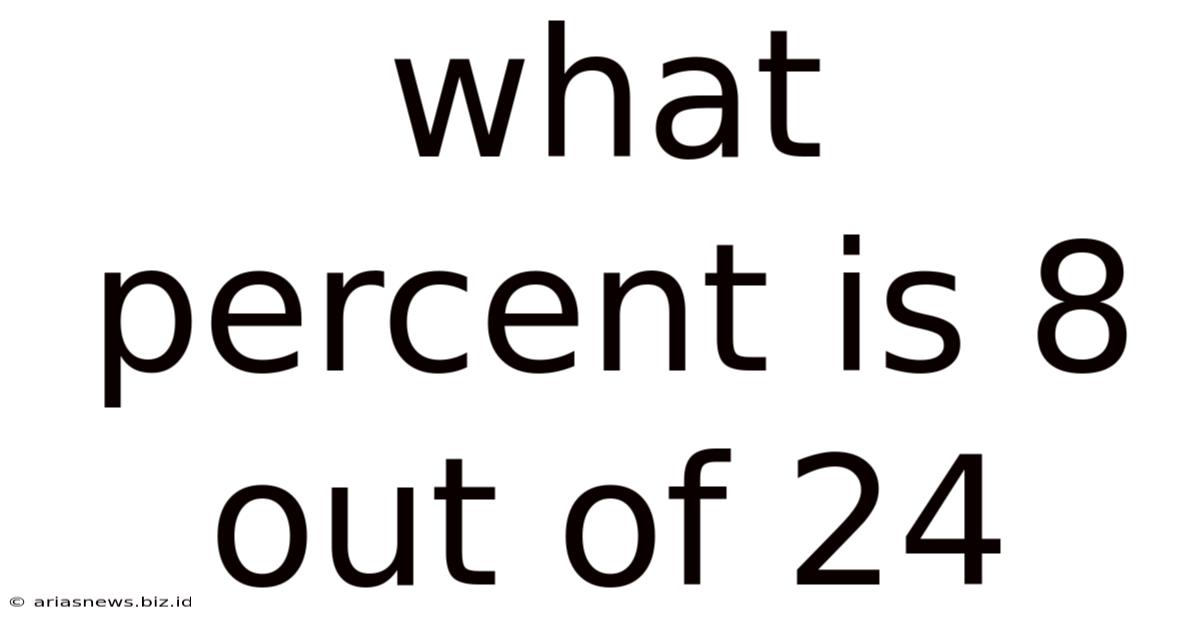
Table of Contents
What Percent is 8 Out of 24? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts in a store to analyzing data in a professional setting. This comprehensive guide delves into the question, "What percent is 8 out of 24?", providing not only the answer but also a thorough explanation of the process, along with practical applications and related concepts.
Calculating the Percentage: A Step-by-Step Approach
The core of solving "What percent is 8 out of 24?" lies in understanding the relationship between parts and wholes. The number 24 represents the whole, or the total amount, while 8 represents a part of that whole. To find the percentage, we need to determine what fraction 8 is of 24, and then convert that fraction into a percentage.
Here's the step-by-step process:
-
Form a Fraction: Express the problem as a fraction. The part (8) becomes the numerator, and the whole (24) becomes the denominator: 8/24.
-
Simplify the Fraction (Optional but Recommended): Simplifying the fraction makes the subsequent calculation easier. Both 8 and 24 are divisible by 8: 8/24 simplifies to 1/3.
-
Convert the Fraction to a Decimal: Divide the numerator (1) by the denominator (3): 1 ÷ 3 = 0.3333... (This decimal is a repeating decimal).
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.3333... × 100 ≈ 33.33%.
Therefore, 8 out of 24 is approximately 33.33%.
Understanding the Concept of Percentage
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." When we say 33.33%, we're saying that for every 100 units, 33.33 units represent the portion we're interested in. This makes percentages a convenient way to compare proportions and make relative comparisons.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios. Consider these examples:
-
Sales and Discounts: Stores frequently advertise discounts as percentages. If a $100 item is discounted by 20%, you can easily calculate the discount amount ($20) and the final price ($80).
-
Grade Calculation: Academic grades are often expressed as percentages. If you scored 18 out of 20 on a test, you can calculate your percentage score (90%) to understand your performance.
-
Financial Analysis: Percentages are used extensively in finance, including calculating interest rates, returns on investments, and analyzing financial statements.
-
Data Analysis and Statistics: Percentages are used to represent proportions in data analysis, helping to visualize and interpret data more effectively.
-
Everyday Life: From calculating tips in restaurants to determining the proportion of ingredients in a recipe, percentages are useful in many daily situations.
Beyond the Basics: Exploring Related Concepts
While calculating "what percent is 8 out of 24" is straightforward, understanding related concepts deepens your understanding of percentage calculations.
1. Finding the Part Given the Percentage and the Whole
Let's say you know that 25% of a certain amount is 15. How would you find the total amount?
-
Set up an equation: Let 'x' represent the total amount. We can write the equation: 0.25x = 15
-
Solve for x: Divide both sides by 0.25: x = 15 / 0.25 = 60
Therefore, the total amount is 60.
2. Finding the Percentage Given the Part and the Whole (Alternative Method)
We already solved this for "8 out of 24," but let's explore an alternative approach using proportions:
-
Set up a proportion: Let 'x' represent the percentage. We can set up the proportion: 8/24 = x/100
-
Cross-multiply: 24x = 800
-
Solve for x: x = 800 / 24 = 33.33%
3. Percentage Increase and Decrease
Percentage increase or decrease calculates the relative change between two values. For example, if a value increases from 50 to 60, the percentage increase is calculated as follows:
-
Find the difference: 60 - 50 = 10
-
Divide the difference by the original value: 10 / 50 = 0.2
-
Multiply by 100 to express as a percentage: 0.2 × 100 = 20%
Therefore, the value increased by 20%. Percentage decrease is calculated similarly, but the difference is subtracted from the original value.
Advanced Applications and Considerations
Percentage calculations extend beyond simple problems. They are fundamental to:
-
Compound Interest: Calculating compound interest requires understanding how percentages accumulate over time.
-
Statistical Analysis: Percentages are essential for representing proportions and interpreting statistical data.
-
Business and Economics: Understanding percentage changes in economic indicators (inflation, GDP growth) is crucial for economic analysis.
-
Scientific Calculations: Many scientific calculations rely on percentage changes and proportions.
Avoiding Common Mistakes
Several common errors can lead to incorrect percentage calculations:
-
Incorrect Order of Operations: Remember to perform division before multiplication when converting fractions to percentages.
-
Confusion with Percentages and Decimals: Accurately convert between decimals and percentages.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with repeating decimals.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, as demonstrated with the example of "What percent is 8 out of 24?", is a crucial life skill. This comprehensive guide not only provided the solution but also explored various applications and related concepts. By mastering these techniques, you'll be well-equipped to tackle various percentage problems and confidently apply this knowledge in diverse contexts, from everyday tasks to complex calculations. Remember to practice regularly to solidify your understanding and enhance your problem-solving abilities.
Latest Posts
Latest Posts
-
Is Pi Over 2 Rational Or Irrational
May 11, 2025
-
Beverly Hill Polo Club Vs Ralph Lauren
May 11, 2025
-
How Many Angles Are In A Circle
May 11, 2025
-
What Color Do You Wear To Church On Palm Sunday
May 11, 2025
-
How Many Pounds Of Peaches In A Half Bushel
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 8 Out Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.