What Percentage Is 11 Out Of 18
Arias News
May 10, 2025 · 5 min read
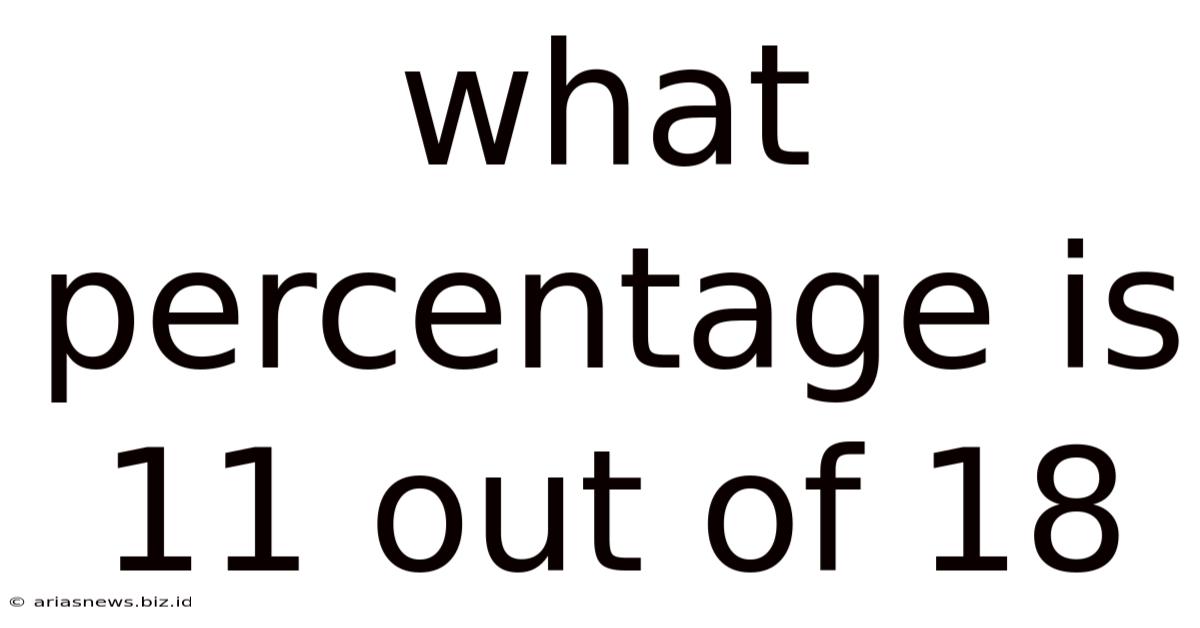
Table of Contents
What Percentage is 11 out of 18? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to more complex scenarios in finance, science, and statistics. Understanding how to determine what percentage 11 out of 18 represents is not just about getting the answer; it's about grasping the underlying principles of percentage calculations and applying them effectively. This comprehensive guide will delve into the process, explore different calculation methods, and provide practical examples to solidify your understanding.
Understanding Percentages
Before we dive into the specifics of calculating 11 out of 18 as a percentage, let's refresh our understanding of what a percentage actually is. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per cent," which literally means "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: The Basic Formula
The most straightforward method to calculate the percentage involves using the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 11
- Whole: 18
Substituting these values into the formula:
(11 / 18) x 100% = ?
Performing the calculation:
0.6111 x 100% ≈ 61.11%
Therefore, 11 out of 18 is approximately 61.11%.
Method 2: Using Decimal Conversion
This method involves converting the fraction to a decimal first and then multiplying by 100%.
-
Convert the fraction to a decimal: Divide the part (11) by the whole (18): 11 ÷ 18 ≈ 0.6111
-
Multiply by 100%: 0.6111 x 100% ≈ 61.11%
This method yields the same result as the basic formula method.
Method 3: Simplifying the Fraction (Optional)
While not strictly necessary, simplifying the fraction before converting to a decimal can sometimes make the calculation easier. In this case, 11/18 doesn't simplify further because 11 is a prime number and doesn't share any common factors with 18. However, let's look at an example where simplification is useful:
Let's say we wanted to find the percentage of 10 out of 20.
-
Simplify the fraction: 10/20 simplifies to 1/2.
-
Convert to decimal: 1 ÷ 2 = 0.5
-
Multiply by 100%: 0.5 x 100% = 50%
This illustrates that simplifying the fraction can streamline the calculation, especially when dealing with larger numbers that share common factors.
Understanding the Result: 61.11%
The result, 61.11%, indicates that 11 represents approximately 61.11% of the total 18. This percentage provides a concise way to express the proportional relationship between the part (11) and the whole (18). This type of calculation is useful in numerous applications.
Practical Applications of Percentage Calculations
The ability to calculate percentages is incredibly versatile and finds application in various fields:
1. Finance and Budgeting:
- Calculating interest rates: Understanding how interest accrues on loans or investments requires percentage calculations.
- Determining discounts: Calculating the price after a discount percentage is a common application.
- Analyzing financial statements: Financial ratios and analyses often involve percentages.
- Tracking spending: Budgeting and tracking spending often involve calculating percentages of income allocated to different categories.
2. Science and Statistics:
- Expressing experimental results: Scientific data is often presented as percentages to show the proportion of successful outcomes or other relevant metrics.
- Calculating probabilities: Percentages are fundamental in expressing probabilities and statistical significance.
- Analyzing survey data: Survey responses are often presented and analyzed as percentages.
3. Everyday Life:
- Calculating tips: Determining the appropriate tip amount in restaurants involves calculating a percentage of the bill.
- Understanding sales tax: Sales tax is a percentage added to the price of goods and services.
- Comparing prices: Comparing prices of similar items often involves calculating percentage differences.
Rounding and Precision
In many real-world situations, it's necessary to round percentages to a specific number of decimal places. The level of precision required depends on the context. For instance, in financial calculations, higher precision is generally needed. For everyday applications, rounding to one or two decimal places is usually sufficient.
In our example (11 out of 18), we rounded the percentage to 61.11%. However, you could round it further to 61% if a less precise result is acceptable.
Avoiding Common Mistakes
- Incorrect order of operations: Always perform the division before multiplying by 100%.
- Incorrect placement of the decimal point: Be mindful of the decimal point when converting from decimal to percentage.
- Rounding errors: Be aware of potential rounding errors, especially when performing multiple calculations.
Advanced Percentage Calculations
While the basic formula provides a solid foundation, more complex scenarios might require advanced techniques, such as:
- Calculating percentage change: Determining the percentage increase or decrease between two values. The formula for percentage change is: [(New Value - Old Value) / Old Value] x 100%.
- Calculating percentage points: This refers to the difference between two percentages, not a percentage change. For example, a change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage.
Conclusion
Calculating what percentage 11 out of 18 represents – approximately 61.11% – is a fundamental skill with far-reaching applications. Understanding the underlying principles of percentage calculations empowers you to tackle various quantitative challenges effectively, from managing your finances to interpreting scientific data and solving everyday problems. By mastering the basic formula and understanding different calculation methods, you'll develop a strong foundation for tackling more complex percentage problems. Remember to always check your work and consider the appropriate level of rounding based on the specific context. With practice, percentage calculations will become second nature.
Latest Posts
Latest Posts
-
How Long Does Miracle Whip Last In The Refrigerator
May 10, 2025
-
Which Statement Most Accurately Describes This Excerpt
May 10, 2025
-
How Do You Say Calculator In Spanish
May 10, 2025
-
How Many Cups Of Mayonnaise In A Jar
May 10, 2025
-
Driving Distance From Nashville Tennessee To Memphis Tennessee
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 11 Out Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.