What Percentage Is 4 Out Of 12
Arias News
Apr 05, 2025 · 5 min read
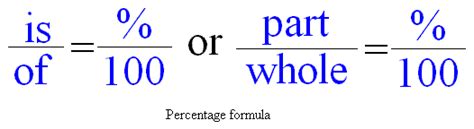
Table of Contents
What Percentage is 4 out of 12? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with broad applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine percentages allows for clear comparisons, informed decision-making, and a deeper understanding of numerical relationships. This comprehensive guide will delve into the specifics of calculating what percentage 4 out of 12 represents, exploring various methods and offering practical examples to solidify your understanding.
Understanding Percentages: The Basics
Before we tackle the specific problem of determining the percentage represented by 4 out of 12, let's establish a firm understanding of what percentages are and how they function.
A percentage is simply a fraction expressed as a part of 100. The symbol "%" denotes this representation. For example, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5. Percentages provide a standardized way to express proportions, making comparisons easier than using fractions or decimals alone.
Key Components of Percentage Calculations:
- Part: This represents the specific portion of the whole you're interested in. In our example, the part is 4.
- Whole: This is the total amount or the complete quantity. In our case, the whole is 12.
- Percentage: This is the value expressed as a part of 100, representing the proportional relationship between the part and the whole. This is what we aim to calculate.
Calculating "What Percentage is 4 out of 12?" - Method 1: The Fraction Method
The most straightforward approach to solving this problem is by converting the given numbers into a fraction and then transforming that fraction into a percentage.
Step 1: Formulate the Fraction:
The first step is to represent the given information as a fraction. The "part" (4) becomes the numerator, and the "whole" (12) becomes the denominator:
4/12
Step 2: Simplify the Fraction (if possible):
Simplifying the fraction often makes the subsequent calculations easier. In this instance, both the numerator and denominator are divisible by 4:
4/12 = 1/3
Step 3: Convert the Fraction to a Decimal:
To convert the simplified fraction to a decimal, divide the numerator by the denominator:
1 ÷ 3 ≈ 0.3333
Step 4: Convert the Decimal to a Percentage:
Finally, multiply the decimal by 100 to express the value as a percentage:
0.3333 x 100 ≈ 33.33%
Therefore, 4 out of 12 is approximately 33.33%.
Calculating "What Percentage is 4 out of 12?" - Method 2: The Direct Percentage Calculation Method
This method bypasses the fraction simplification step and directly calculates the percentage.
Step 1: Set up the Equation:
We can represent the problem as a proportion:
(Part / Whole) x 100 = Percentage
Step 2: Substitute the Values:
Substitute the values from the problem into the equation:
(4 / 12) x 100 = Percentage
Step 3: Calculate the Percentage:
Perform the calculation:
(4 / 12) x 100 = 0.3333 x 100 ≈ 33.33%
Again, we arrive at the same conclusion: 4 out of 12 is approximately 33.33%.
Understanding Recurring Decimals and Rounding
Notice that the decimal representation of 1/3 (0.3333...) is a recurring decimal, meaning the digit 3 repeats infinitely. In practical applications, we usually round this to a certain number of decimal places. For most purposes, rounding to two decimal places (33.33%) is sufficient. However, the level of precision required depends on the context of the calculation.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial for a multitude of everyday scenarios, including:
- Financial Management: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentage calculations.
- Sales and Marketing: Tracking sales performance, analyzing conversion rates, and determining the effectiveness of marketing campaigns relies heavily on percentages.
- Science and Research: Expressing experimental results, analyzing statistical data, and calculating error margins often require the use of percentages.
- Education: Grading systems, performance evaluations, and statistical analysis in educational research heavily utilize percentages.
- Everyday Life: Calculating tips at restaurants, understanding discounts in stores, and interpreting survey results all involve percentage calculations.
Advanced Percentage Calculations: Beyond the Basics
While the example of 4 out of 12 is relatively simple, percentage calculations can become more complex. Here are some more advanced scenarios:
- Calculating Percentage Increase or Decrease: This involves determining the percentage change between two values. For instance, if a price increases from $10 to $15, the percentage increase is calculated as [(15-10)/10] x 100 = 50%.
- Calculating Percentage of a Percentage: This involves calculating a percentage of another percentage. For example, finding 20% of 50% would be 0.20 x 0.50 x 100 = 10%.
- Working with Multiple Percentages: Some problems involve combining or comparing multiple percentages. For example, calculating the final price after applying multiple discounts or taxes.
- Using Percentages in Equations: Percentages can be incorporated into more complex algebraic equations to solve various problems.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more confident and proficient you'll become.
- Utilize online calculators and resources: Many online resources can help you verify your calculations and explore different approaches.
- Understand the underlying concepts: A thorough understanding of fractions, decimals, and proportions is essential for mastering percentage calculations.
- Break down complex problems: Divide complex problems into smaller, manageable steps to avoid errors.
- Check your work: Always double-check your calculations to ensure accuracy.
Conclusion: The Power of Percentages
Understanding how to calculate percentages, as exemplified by the problem "What percentage is 4 out of 12?", is a fundamental skill with wide-ranging applications. By mastering these calculations, you equip yourself with a powerful tool for navigating various aspects of life, from personal finance to professional endeavors. Remember to practice regularly and break down complex problems into smaller, more manageable steps to build your proficiency and confidence in handling percentages. This skill will undoubtedly enhance your ability to interpret data, make informed decisions, and succeed in various fields.
Latest Posts
Latest Posts
-
What Does S And M Mean In The Song
Apr 05, 2025
-
What Is The Melting Point Of Ice
Apr 05, 2025
-
What Is A 16 Out Of 23
Apr 05, 2025
-
El Burro Sabe Mas Que Maduro Translate To English
Apr 05, 2025
-
How Big Is Scotland Compared To Texas
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 4 Out Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
