Whats 3 To The Power Of 3
Arias News
Apr 05, 2025 · 6 min read
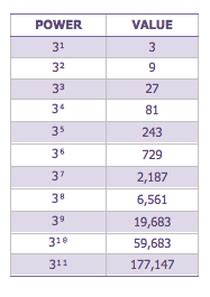
Table of Contents
What's 3 to the Power of 3? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What's 3 to the power of 3?" opens a door to a vast world of mathematical concepts, their practical applications, and their significance in various fields. While the answer itself is straightforward (27), the journey to understanding why and how we arrive at this answer, and the broader implications of exponentiation, is far more enriching. This article will delve into the meaning of exponents, explore different ways to calculate 3³, discuss its relevance in various fields, and finally, touch upon more advanced concepts related to exponentiation.
Understanding Exponents: The Basics
Before we tackle 3³, let's establish a solid foundation in exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. The general form is represented as b<sup>n</sup>, where 'b' is the base and 'n' is the exponent. This means b<sup>n</sup> = b × b × b × ... × b (n times).
For instance:
- 2<sup>2</sup> (2 to the power of 2, or 2 squared) = 2 × 2 = 4
- 5<sup>3</sup> (5 to the power of 3, or 5 cubed) = 5 × 5 × 5 = 125
- 10<sup>4</sup> (10 to the power of 4) = 10 × 10 × 10 × 10 = 10,000
Therefore, 3<sup>3</sup> (3 to the power of 3, or 3 cubed) simply means 3 multiplied by itself three times: 3 × 3 × 3 = 27.
Calculating 3³: Multiple Approaches
While the direct calculation (3 × 3 × 3 = 27) is the most straightforward method, let's explore alternative approaches to solidify our understanding:
-
Repeated Multiplication: As shown above, this is the most fundamental method. It involves sequentially multiplying the base number by itself the number of times specified by the exponent.
-
Using a Calculator: Most calculators have an exponent function (usually denoted by a ^ symbol or a button labeled x<sup>y</sup>). Simply input 3 ^ 3 or 3 x<sup>y</sup> 3 to obtain the result, 27.
-
Logarithms (for more advanced understanding): While not necessary for calculating 3³, logarithms provide an inverse operation to exponentiation. If we had the equation x = 3³, we could use logarithms to solve for x by taking the logarithm base 3 of both sides: log<sub>3</sub>(x) = 3. This would yield x = 27. This approach is more useful for solving more complex exponential equations.
The Significance of 3³ and Cubic Relationships
The result of 3³ = 27 has various applications and symbolic meanings across different fields:
-
Geometry: In three-dimensional geometry, 27 represents the volume of a cube with side length 3 units. This is a direct application of the concept of cubing—calculating the volume of a three-dimensional object with equal sides.
-
Number Theory: 27 is a perfect cube (3³), a significant concept in number theory. Perfect cubes are numbers that can be obtained by raising an integer to the power of 3. Understanding perfect cubes is fundamental for various mathematical proofs and problem-solving.
-
Combinatorics and Probability: The number 27 can appear in combinatorial problems where we need to arrange or select items. For example, consider choosing 3 items from a set of 3 distinct items with replacement; the number of possible combinations will involve powers and could potentially lead to a calculation related to 3³.
-
Physics and Engineering: Cubic relationships appear frequently in physics and engineering, such as calculating the volume of objects, the relationship between power and current in electrical circuits (P = I³R), and in various formulas related to fluid dynamics and thermodynamics.
Expanding the Concept: Higher Powers and Fractional Exponents
While we've focused on 3³, the principles of exponentiation extend to much larger numbers and even fractional and negative exponents:
-
Higher Powers: Calculating 3<sup>4</sup>, 3<sup>5</sup>, and so on, simply involves extending the repeated multiplication process. 3<sup>4</sup> = 3 × 3 × 3 × 3 = 81, 3<sup>5</sup> = 243, and so forth.
-
Fractional Exponents: Fractional exponents introduce the concept of roots. For example, 3<sup>1/2</sup> represents the square root of 3, approximately 1.732. Similarly, 3<sup>1/3</sup> is the cube root of 3, approximately 1.442. A fractional exponent like 3<sup>2/3</sup> can be interpreted as the cube root of 3 squared, or (3²)<sup>1/3</sup> = (9)<sup>1/3</sup> ≈ 2.08.
-
Negative Exponents: Negative exponents represent the reciprocal of the positive exponent. For example, 3<sup>-1</sup> = 1/3, 3<sup>-2</sup> = 1/3² = 1/9, and so on.
Practical Applications Across Disciplines
The understanding and application of exponents, extending beyond the simple calculation of 3³, permeate various fields:
-
Finance and Investment: Compound interest calculations rely heavily on exponents. The formula A = P(1 + r/n)^(nt) shows how an initial investment (P) grows over time (t) with an interest rate (r) compounded n times per year.
-
Computer Science: Exponentiation is fundamental in algorithms, especially those related to data structures like trees and graphs. Computational complexity is often expressed using big O notation, which involves exponential functions.
-
Biology and Medicine: Exponential growth and decay models are used to describe population dynamics, bacterial growth, radioactive decay, and drug absorption/elimination in the body.
-
Social Sciences: Exponential models are applied in studying population growth, the spread of diseases, and the diffusion of information or ideas.
-
Chemistry: Exponents appear in chemical kinetics, describing reaction rates and equilibrium constants.
-
Environmental Science: Exponential decay models are used in describing the rate at which pollutants are removed from the environment.
Beyond the Basics: Exponential Functions and Their Graphs
Moving beyond the specific calculation of 3³, let's consider the broader concept of exponential functions. An exponential function is a function of the form f(x) = a<sup>x</sup>, where 'a' is a constant base (a > 0 and a ≠ 1). The graph of an exponential function exhibits exponential growth (if a > 1) or exponential decay (if 0 < a < 1).
The graph of y = 3<sup>x</sup>, for example, shows exponential growth, with the y-values increasing rapidly as x increases. Understanding the properties of exponential functions is crucial for modeling various phenomena characterized by rapid growth or decay.
Conclusion: The Power of Understanding Exponents
The seemingly simple question, "What's 3 to the power of 3?" serves as a gateway to a deeper appreciation of exponents and their profound influence across numerous disciplines. From calculating the volume of a cube to modeling complex phenomena in finance, biology, and computer science, the concept of exponentiation underlies many fundamental calculations and theoretical frameworks. By grasping the core principles of exponents and their various applications, we equip ourselves with powerful tools for understanding and solving problems in a wide range of fields. The seemingly simple answer, 27, therefore, holds within it a wealth of mathematical richness and practical significance.
Latest Posts
Latest Posts
-
How Far Is A Half A Mile
Apr 05, 2025
-
How Thick Is A Dime In Inches
Apr 05, 2025
-
What If A Man Calls You Honey
Apr 05, 2025
-
What Is The Average Iq Of A 12 Year Old Female
Apr 05, 2025
-
How Many Laps Around A Baseball Field Is A Mile
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Whats 3 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
