Whats 5 To The Power Of 5
Arias News
May 12, 2025 · 5 min read
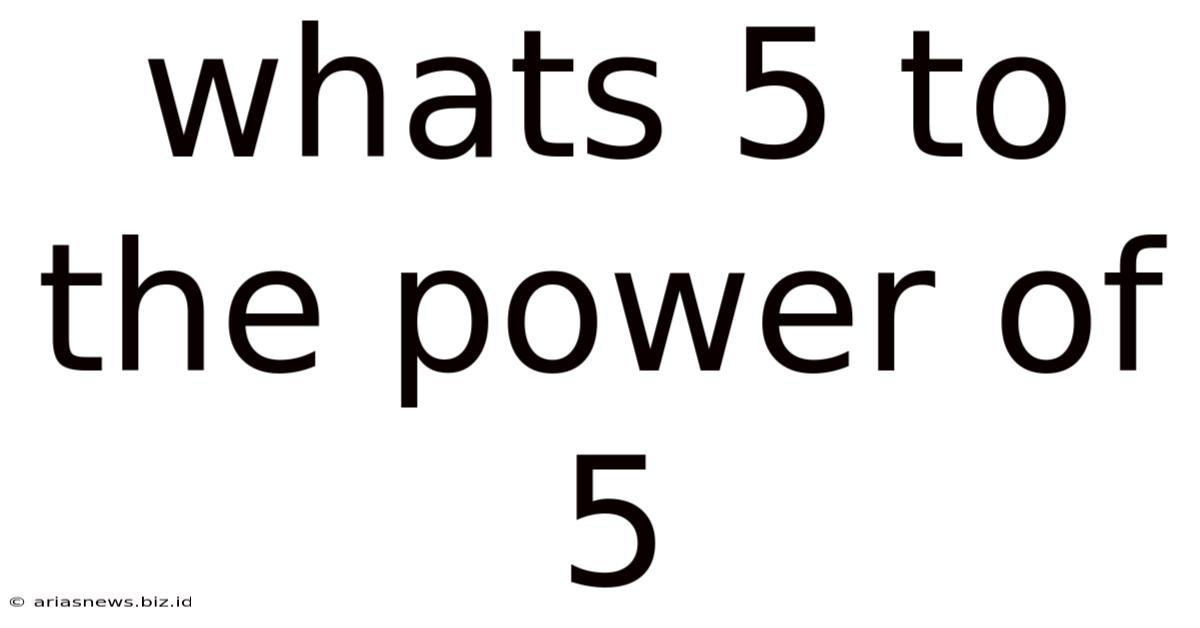
Table of Contents
What's 5 to the Power of 5? Unpacking Exponents and Their Applications
What is 5 to the power of 5? The simple answer is 3125. But this seemingly straightforward calculation opens a door to a fascinating world of exponents, their properties, and their widespread applications across numerous fields. This article will delve deep into the concept of exponentiation, specifically focusing on 5⁵, exploring its mathematical underpinnings, and showcasing its relevance in various real-world scenarios.
Understanding Exponents: A Foundation
Before we delve into the specifics of 5⁵, let's establish a strong understanding of exponents. In mathematics, an exponent (also known as a power or index) represents the number of times a base number is multiplied by itself. The general form is expressed as bⁿ, where 'b' is the base and 'n' is the exponent.
For example, in 5⁵, 5 is the base and 5 is the exponent. This means we multiply 5 by itself five times: 5 x 5 x 5 x 5 x 5 = 3125.
This seemingly simple concept has far-reaching implications, extending beyond basic arithmetic. Let's examine some fundamental properties of exponents:
-
Product of Powers: When multiplying two terms with the same base, you add the exponents: bᵐ x bⁿ = bᵐ⁺ⁿ. For instance, 5² x 5³ = 5⁵ = 3125.
-
Quotient of Powers: When dividing two terms with the same base, you subtract the exponents: bᵐ / bⁿ = bᵐ⁻ⁿ. For example, 5⁵ / 5² = 5³ = 125.
-
Power of a Power: When raising a power to another power, you multiply the exponents: (bᵐ)ⁿ = bᵐⁿ. For example, (5²)³ = 5⁶ = 15625.
-
Power of a Product: When raising a product to a power, you raise each factor to that power: (ab)ⁿ = aⁿbⁿ. For example, (2 x 5)³ = 2³ x 5³ = 8 x 125 = 1000.
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power: (a/b)ⁿ = aⁿ/bⁿ (assuming b ≠ 0). For example, (5/2)² = 5²/2² = 25/4 = 6.25.
Calculating 5⁵: Methods and Approaches
Calculating 5⁵ can be done in several ways:
-
Direct Multiplication: This is the most straightforward approach: 5 x 5 x 5 x 5 x 5 = 3125. This method is easily done with a calculator or by hand for smaller exponents.
-
Using the Properties of Exponents: As discussed above, you can break down the calculation using exponent properties. For example, you could calculate 5² = 25, then 25² = 625, and finally 625 x 5 = 3125. This method is helpful for larger exponents or when dealing with more complex expressions.
-
Using Logarithms: While not the most intuitive method for this specific calculation, logarithms can be useful for larger exponents or for solving equations where the exponent is unknown. The logarithm base 5 of 3125 is 5 (log₅3125 = 5).
-
Using a Calculator or Computer: Modern calculators and computer software can easily handle exponentiation calculations, providing a quick and accurate result.
The Significance of 3125: Applications Across Disciplines
The result of 5⁵, 3125, while seemingly a simple number, has relevance in various fields:
-
Computer Science: In binary systems, numbers are represented using powers of 2. While 3125 isn't directly a power of 2, understanding exponentiation is crucial for binary arithmetic, memory allocation, and data structures. The efficiency of algorithms often hinges on exponential growth or decay.
-
Finance: Compound interest calculations rely heavily on exponents. The formula for compound interest involves raising the principal amount to a power representing the number of compounding periods. Understanding this principle allows for accurate financial forecasting and investment planning.
-
Physics and Engineering: Exponential functions model various physical phenomena, such as radioactive decay, population growth, and the cooling of objects. The principles of exponentiation are fundamental to understanding and predicting these processes.
-
Biology: Exponential growth is a key concept in population dynamics, describing the rapid increase in the size of a population under ideal conditions. Understanding exponential functions is crucial for modeling population growth in various species.
-
Cryptography: Exponentiation forms the basis of many modern cryptographic algorithms, ensuring the security of online transactions and communications. The difficulty of calculating large exponents underlies the strength of these systems.
Beyond 5⁵: Exploring Larger Exponents and Their Implications
The concept of exponentiation extends far beyond 5⁵. Consider the implications of larger exponents:
-
Exponential Growth: As the exponent increases, the value grows incredibly rapidly. This rapid growth is often visualized using exponential curves, which show an increasingly steep incline. Understanding this rapid growth is essential for predicting trends in various fields, from population growth to technological advancements.
-
Exponential Decay: Conversely, negative exponents represent decay, where the value decreases rapidly. This is evident in phenomena like radioactive decay, where the amount of radioactive material decreases exponentially over time.
-
Fractional Exponents: Exponents can also be fractions, representing roots. For example, 5^(1/2) is the square root of 5, and 5^(1/3) is the cube root of 5. Fractional exponents allow for the calculation of roots and provide a powerful tool for solving various mathematical problems.
Conclusion: The Ubiquity of Exponentiation
The seemingly simple calculation of 5⁵ = 3125 unveils a much deeper mathematical concept—exponentiation—with wide-ranging applications across diverse disciplines. From finance and computer science to biology and physics, understanding exponents is essential for comprehending and modeling numerous real-world phenomena. The principles discussed in this article provide a solid foundation for further exploration of exponential functions, their properties, and their crucial role in solving complex problems. The power of 5⁵, therefore, extends far beyond its numerical value, representing a fundamental concept with far-reaching significance in our understanding of the world around us. Further exploration into logarithmic functions and their inverse relationship with exponential functions will also deepen your understanding of this critical mathematical concept. Remember to practice various problems involving exponents to solidify your understanding and develop your problem-solving skills.
Latest Posts
Latest Posts
-
Why Does Beowulf Put Aside His Weapons And Armor
May 12, 2025
-
What Side Does The Napkin Go On A Place Setting
May 12, 2025
-
Gifts That Begin With The Letter Y
May 12, 2025
-
A House Of A Rabbit Is Called
May 12, 2025
-
How Many Oz Is A Sweet Potato
May 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 5 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.