What's The Sum Of 3/8 And 1/16
Arias News
May 11, 2025 · 6 min read
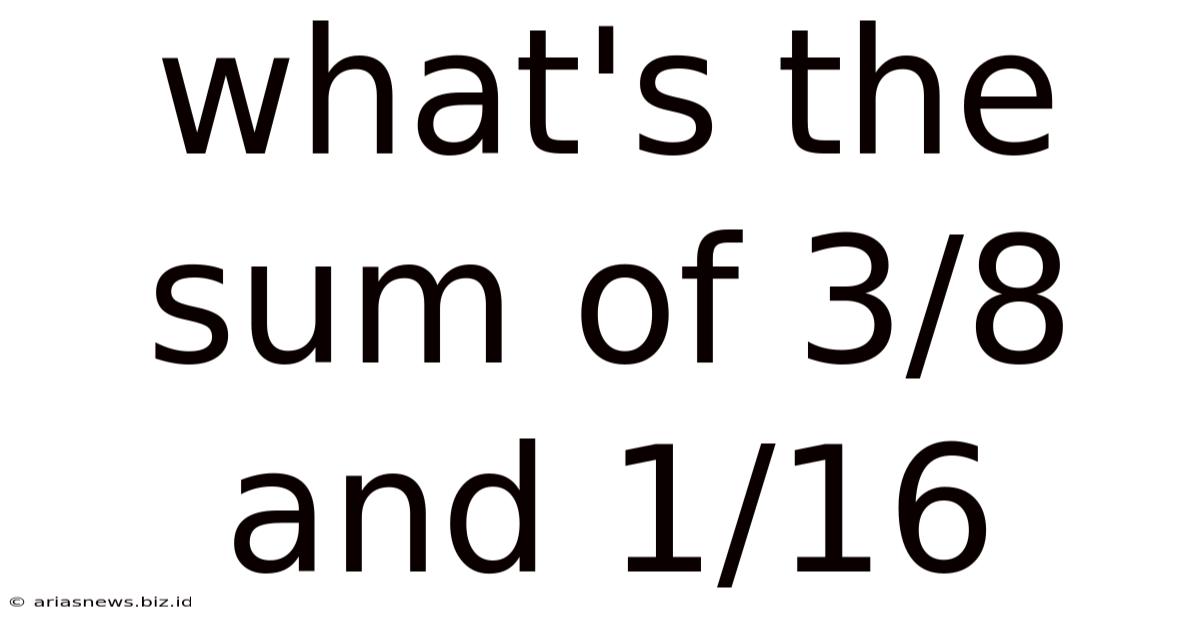
Table of Contents
What's the Sum of 3/8 and 1/16? A Deep Dive into Fraction Addition
Adding fractions might seem like a simple arithmetic task, but understanding the underlying principles is crucial for mastering more complex mathematical concepts. This comprehensive guide will not only solve the equation 3/8 + 1/16 but also delve into the fundamental concepts of fraction addition, offering practical examples and strategies to enhance your understanding.
Understanding Fractions: A Quick Refresher
Before we tackle the addition problem, let's briefly review the components of a fraction. A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The top number represents the number of parts you have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 3/8, 3 is the numerator (the number of parts you have), and 8 is the denominator (the total number of equal parts).
Finding a Common Denominator: The Key to Fraction Addition
The fundamental rule of adding fractions is that they must have the same denominator. If the denominators are different, you need to find a common denominator before you can add the numerators. This common denominator is a multiple of both original denominators. The least common multiple (LCM) is the smallest such multiple and is often the most efficient choice.
Let's illustrate this with our example: 3/8 + 1/16. The denominators are 8 and 16. We need to find a common denominator for both.
- Multiples of 8: 8, 16, 24, 32...
- Multiples of 16: 16, 32, 48...
Notice that 16 is a multiple of 8. Therefore, 16 is the least common multiple (LCM) and our common denominator.
Converting Fractions to a Common Denominator
Now that we have a common denominator (16), we need to convert both fractions so they have this denominator.
To convert 3/8 to a fraction with a denominator of 16, we ask: "What number multiplied by 8 equals 16?" The answer is 2. Therefore, we multiply both the numerator and the denominator of 3/8 by 2:
(3/8) * (2/2) = 6/16
The fraction 1/16 already has the denominator of 16, so it doesn't need to be changed.
Adding the Fractions
Now that both fractions have the same denominator (16), we can add them by simply adding their numerators:
6/16 + 1/16 = (6 + 1)/16 = 7/16
Therefore, the sum of 3/8 and 1/16 is 7/16.
Simplifying Fractions: Reducing to Lowest Terms
After adding fractions, it's important to check if the resulting fraction can be simplified. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
In our case, the fraction is 7/16. The only factors of 7 are 1 and 7, and 7 is not a factor of 16. Therefore, 7/16 is already in its simplest form.
Real-World Applications of Fraction Addition
Adding fractions isn't just an abstract mathematical exercise; it has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Adding fractions is essential to accurately calculate the total amount of an ingredient needed. For instance, combining 1/2 cup of sugar with 1/4 cup of sugar would require knowing how to add fractions.
-
Construction and Engineering: Accurate measurements are critical in construction and engineering projects. Fractions are frequently used to represent dimensions and measurements, requiring addition and subtraction of fractions for precise calculations.
-
Finance and Budgeting: Managing personal finances often involves working with fractions of money. Adding fractions helps to calculate total expenses or portions of savings.
-
Data Analysis and Statistics: Many statistical calculations involve the use of fractions and the addition of fractional data points.
Advanced Techniques for Fraction Addition
While the method explained above works effectively for simpler fractions, some situations might require more advanced techniques:
-
Finding the LCM for larger numbers: For fractions with larger denominators, finding the least common multiple might be more challenging. Using prime factorization or other techniques can simplify this process.
-
Adding more than two fractions: The same principles apply when adding more than two fractions. Find a common denominator for all fractions and then add the numerators.
-
Mixed numbers: A mixed number consists of a whole number and a fraction (e.g., 2 1/2). To add mixed numbers, you can convert them into improper fractions (where the numerator is greater than the denominator) before adding them using the standard method.
-
Subtracting fractions: Subtracting fractions follows similar rules, but you subtract the numerators instead of adding them after finding a common denominator.
Troubleshooting Common Mistakes in Fraction Addition
-
Forgetting to find a common denominator: This is the most frequent mistake. Always ensure that fractions have a common denominator before adding their numerators.
-
Incorrectly converting to a common denominator: Pay close attention to the multiplication process when converting fractions to a common denominator. Make sure you multiply both the numerator and the denominator by the same number.
-
Adding denominators: Remember, you only add the numerators; the denominator remains the same.
-
Not simplifying the answer: Always simplify the resulting fraction to its lowest terms for a complete and accurate answer.
Practicing Fraction Addition: Tips and Exercises
The key to mastering fraction addition is practice. Here are some tips to improve your skills:
-
Start with simple fractions: Begin by practicing with fractions that have small denominators.
-
Work through examples step-by-step: Follow each step carefully to understand the process.
-
Create your own practice problems: Make up your own fraction addition problems to reinforce your understanding.
-
Use visual aids: Diagrams or visual representations can help you understand the concept of fractions and fraction addition more easily.
Here are a few practice problems:
- 1/4 + 2/8
- 3/5 + 1/10
- 2/3 + 1/6 + 1/2
- 1 1/2 + 2/3
Remember, the goal is not just to get the correct answer but to understand the underlying principles and develop a strong foundation in fraction arithmetic.
Conclusion: Mastering the Art of Fraction Addition
Adding fractions, although seemingly simple, requires a thorough understanding of fundamental principles. By mastering the techniques of finding common denominators, converting fractions, and simplifying results, you’ll be able to tackle more complex mathematical problems with confidence. Consistent practice and a focus on understanding the underlying concepts are key to success. The sum of 3/8 and 1/16, as we've shown, is 7/16 – a seemingly small calculation with far-reaching implications in various fields. This detailed explanation aims to equip you with the knowledge and tools to confidently handle fraction addition in any context. Keep practicing, and you'll soon be a fraction addition expert!
Latest Posts
Latest Posts
-
What Does An Equal Sign With 3 Lines Mean
May 12, 2025
-
What Is One Of The Common Characteristics Of Hindu Art
May 12, 2025
-
What Is 20 To The Power Of 2
May 12, 2025
-
How Much Potato Salad For 150 Guests
May 12, 2025
-
Should Color And Design Be Used In Emails
May 12, 2025
Related Post
Thank you for visiting our website which covers about What's The Sum Of 3/8 And 1/16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.