Which Is Bigger 1 4 Or 1 8
Arias News
Apr 06, 2025 · 5 min read
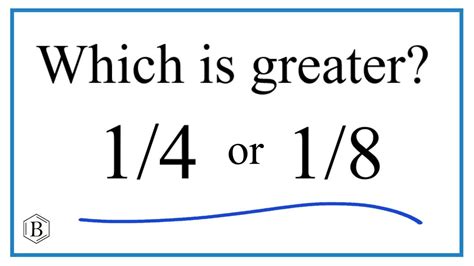
Table of Contents
Which is Bigger: 1/4 or 1/8? A Deep Dive into Fractions
Understanding fractions is fundamental to mathematics, and comparing them is a crucial skill. This seemingly simple question – which is bigger, 1/4 or 1/8? – provides a perfect opportunity to explore the world of fractions, delve into different methods of comparison, and ultimately build a stronger foundation in mathematical reasoning. This in-depth article will not only answer the question directly but also explore the underlying concepts, providing you with the tools to confidently compare any two fractions.
Visualizing Fractions: The Power of Representation
The most intuitive way to understand which fraction is larger, 1/4 or 1/8, is through visualization. Imagine a pizza cut into four equal slices (1/4) and another identical pizza cut into eight equal slices (1/8).
The Pizza Analogy: A Simple Comparison
- 1/4: One slice out of four equal slices represents a larger portion of the pizza.
- 1/8: One slice out of eight equal slices represents a smaller portion of the pizza.
This visual representation clearly demonstrates that 1/4 is larger than 1/8. The fewer slices a pizza is divided into, the larger each individual slice becomes.
The Mathematical Approach: Comparing Fractions with Different Denominators
While visualization is helpful, a more robust method is required for comparing fractions with different denominators. Let's explore several methods:
Method 1: Finding a Common Denominator
The most common method involves finding a common denominator. A common denominator is a number that is divisible by both denominators (the bottom numbers of the fractions). In this case, the denominators are 4 and 8.
- The least common multiple (LCM) of 4 and 8 is 8.
Now, we convert both fractions to have a denominator of 8:
- 1/4: To get a denominator of 8, we multiply both the numerator and denominator by 2: (1 x 2) / (4 x 2) = 2/8
- 1/8: This fraction already has a denominator of 8.
Now we compare 2/8 and 1/8. Since 2 is greater than 1, 2/8 (equivalent to 1/4) is greater than 1/8.
Method 2: Converting to Decimals
Another approach is to convert the fractions to decimals. This can be easily done by dividing the numerator by the denominator:
- 1/4 = 0.25
- 1/8 = 0.125
Comparing the decimal values, it's clear that 0.25 is greater than 0.125, reinforcing that 1/4 is larger than 1/8.
Method 3: Cross-Multiplication
Cross-multiplication provides a direct method for comparing fractions. This method involves multiplying the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then, compare the products.
-
1/4 vs 1/8
-
Cross-multiply: (1 x 8) = 8 and (1 x 4) = 4
Since 8 > 4, 1/4 is greater than 1/8.
Beyond the Basics: Extending the Concept
While the comparison of 1/4 and 1/8 is relatively straightforward, the principles involved apply to comparing any two fractions, regardless of their complexity. Let's extend our understanding with some examples:
Example 1: Comparing Fractions with Larger Numerators
Let's compare 3/4 and 5/8. Using the common denominator method:
- The LCM of 4 and 8 is 8.
- 3/4 = (3 x 2) / (4 x 2) = 6/8
- 5/8 remains 5/8.
Since 6/8 > 5/8, 3/4 is greater than 5/8.
Example 2: Comparing Fractions with Different Denominators and Numerators
Let's compare 7/12 and 2/3.
- The LCM of 12 and 3 is 12.
- 2/3 = (2 x 4) / (3 x 4) = 8/12
- 7/12 remains 7/12.
Since 8/12 > 7/12, 2/3 is greater than 7/12.
Example 3: Improper Fractions and Mixed Numbers
The same principles apply to improper fractions (where the numerator is larger than the denominator) and mixed numbers (a whole number and a fraction). First, convert mixed numbers to improper fractions before comparison. For example, comparing 1 1/2 and 2 1/4:
- 1 1/2 = 3/2
- 2 1/4 = 9/4
Find a common denominator (4):
- 3/2 = 6/4
- 9/4 remains 9/4.
Therefore, 2 1/4 is greater than 1 1/2.
Real-World Applications: Fractions in Everyday Life
Understanding fraction comparison isn't just an academic exercise. It has numerous practical applications in daily life:
- Cooking and Baking: Following recipes often requires understanding fractions (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt).
- Measuring and Construction: Accurate measurements in construction and other trades depend heavily on fractions of inches or centimeters.
- Finance and Budgeting: Managing finances involves understanding fractions of dollars or percentages (which are essentially fractions based on 100).
- Data Analysis: Interpreting data often involves working with fractions and proportions.
Conclusion: Mastering Fraction Comparison
The ability to compare fractions accurately is a cornerstone of mathematical literacy. By understanding the various methods—visualization, finding a common denominator, converting to decimals, and cross-multiplication—you can confidently tackle any fraction comparison problem. Remember, the key is to develop a systematic approach and choose the method that best suits the given fractions. The more you practice, the more intuitive and effortless this skill will become, paving the way for more advanced mathematical concepts. This understanding extends beyond simple comparisons, forming a crucial foundation for algebra, calculus, and countless other mathematical applications throughout your life.
Latest Posts
Latest Posts
-
10 Out Of 14 As A Percentage
Apr 07, 2025
-
How Many Centimeters Are In 13 Meters
Apr 07, 2025
-
What Is A Producer In The Tundra
Apr 07, 2025
-
What Is A Suffix On An Application
Apr 07, 2025
-
What Theme Is Supported By The Excerpt
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 1 4 Or 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
