Which Is Larger 3 4 Or 7 8
Arias News
May 10, 2025 · 5 min read
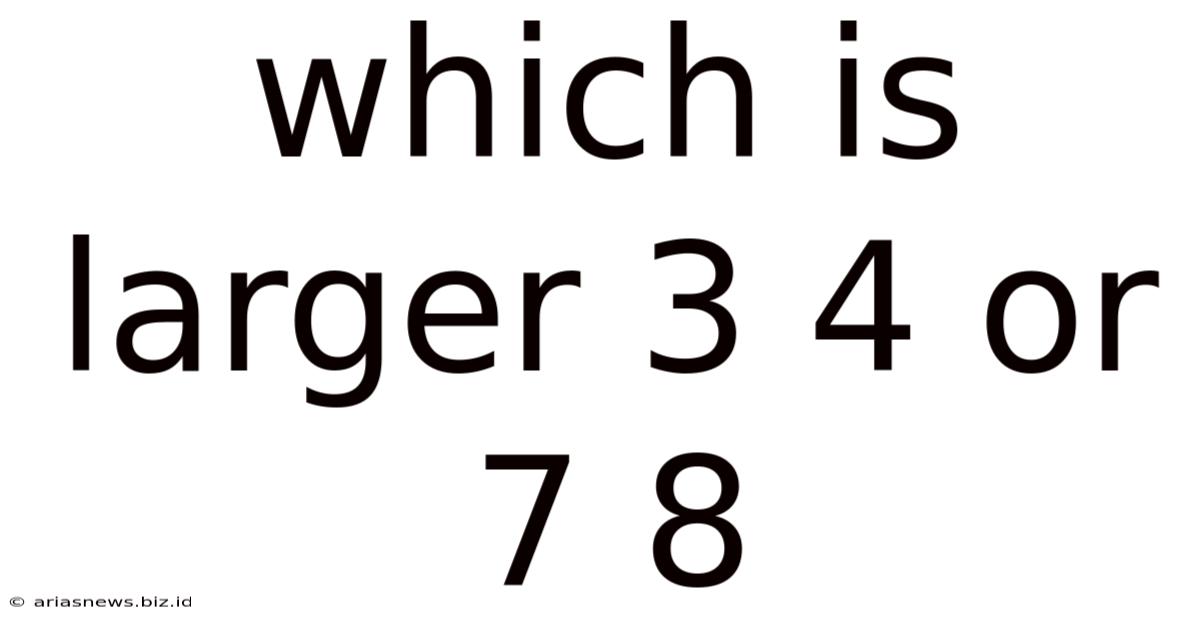
Table of Contents
Which is Larger: 3/4 or 7/8? A Deep Dive into Fraction Comparison
Determining which fraction is larger, 3/4 or 7/8, might seem straightforward at first glance. However, a deeper understanding of fractions and various comparison methods unveils valuable insights into fundamental mathematical concepts. This article will not only answer the question directly but also explore multiple approaches to comparing fractions, providing a comprehensive understanding for students and enthusiasts alike.
Understanding Fractions
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents three parts, and the denominator (4) signifies that the whole is divided into four equal parts.
Method 1: Finding a Common Denominator
This is a classic and reliable method for comparing fractions. The core idea is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 3/4 and 7/8, we look for the least common multiple (LCM) of 4 and 8. Since 8 is a multiple of 4 (4 x 2 = 8), the LCM is 8.
- We leave 7/8 as it is, as its denominator is already 8.
- To convert 3/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 2: (3 x 2) / (4 x 2) = 6/8.
Now we can easily compare 6/8 and 7/8. Since 7 > 6, we conclude that 7/8 is larger than 3/4.
Method 2: Converting to Decimals
Another effective approach is to convert both fractions into decimals. This method is particularly helpful when dealing with fractions that don't easily share a common denominator or when using a calculator.
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
- 3/4 = 3 ÷ 4 = 0.75
- 7/8 = 7 ÷ 8 = 0.875
Comparing the decimal values, 0.875 > 0.75, confirming that 7/8 is larger than 3/4.
Method 3: Visual Representation
While less precise for complex fractions, visualizing fractions can be incredibly intuitive, especially for beginners. Imagine two identical pizzas.
- One pizza is divided into four equal slices, and you have three of them (3/4).
- The other pizza is divided into eight equal slices, and you have seven of them (7/8).
By visually comparing the portions, it becomes clear that seven slices out of eight (7/8) represent a larger portion than three slices out of four (3/4). This visual approach solidifies the understanding of the fraction comparison.
Method 4: Cross-Multiplication
This method provides a quick and efficient way to compare two fractions without finding a common denominator. It involves multiplying the numerator of one fraction by the denominator of the other, and vice-versa.
Let's compare 3/4 and 7/8 using cross-multiplication:
- Multiply the numerator of the first fraction (3) by the denominator of the second fraction (8): 3 x 8 = 24.
- Multiply the numerator of the second fraction (7) by the denominator of the first fraction (4): 7 x 4 = 28.
Compare the results: 24 < 28. Since the product involving 7/8 (28) is larger, 7/8 is the larger fraction.
Extending the Understanding: Fraction Comparisons in Real-World Applications
The ability to compare fractions is not just an academic exercise; it has practical applications in various real-world scenarios:
- Baking: Recipes often require precise measurements using fractions. Comparing fractions ensures accurate ingredient proportions.
- Construction: Accurate measurements are crucial in construction projects. Understanding fraction comparison allows for precise calculations and avoids errors.
- Finance: Understanding fractions is essential in calculating interest rates, percentages, and proportions of investments.
- Data Analysis: In data analysis, fractions frequently represent proportions or percentages within datasets. Accurate comparisons are key to drawing meaningful conclusions.
Addressing Common Misconceptions
A common mistake when comparing fractions is focusing solely on the numerators or denominators without considering both. For example, some might incorrectly assume that 3/4 is larger because 3 > 2 (the numerator in 2/3), neglecting the difference in denominators.
Another misconception arises when attempting to compare fractions with different denominators without employing a proper comparison method. Simply looking at the fractions without finding a common denominator or converting to decimals can lead to inaccurate conclusions.
Further Exploration: Comparing More Than Two Fractions
The methods discussed above can be extended to compare more than two fractions. For multiple fractions, finding the least common denominator for all fractions is the most reliable approach before comparing the numerators. Similarly, converting all fractions to decimals allows for a straightforward comparison.
Conclusion: Mastering Fraction Comparison
This article comprehensively explored various methods for comparing fractions, focusing on the specific comparison of 3/4 and 7/8. Through the use of common denominators, decimal conversion, visual representation, and cross-multiplication, we definitively established that 7/8 is larger than 3/4. Understanding these methods is crucial not only for solving mathematical problems but also for applying fraction comparison in real-world scenarios. By grasping these concepts, you enhance your mathematical skills and broaden your problem-solving capabilities. Remember that consistent practice is key to mastering fraction comparison and solidifying your understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Why Is The Converse Logo On The Inside
May 10, 2025
-
Lines That Intersect At A 90 Degree Angle
May 10, 2025
-
How Many Millimeters Are In 12 Centimeters
May 10, 2025
-
How Many Cubic Centimeters In A Centimeter
May 10, 2025
-
Which Is Longer A Meter Or A Kilometer
May 10, 2025
Related Post
Thank you for visiting our website which covers about Which Is Larger 3 4 Or 7 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.