Which Is Larger 5 8 Or 1 2
Arias News
Mar 28, 2025 · 5 min read
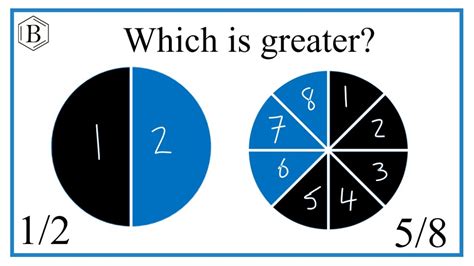
Table of Contents
Which is Larger: 5/8 or 1/2? A Deep Dive into Fraction Comparison
Determining which fraction is larger, 5/8 or 1/2, might seem like a simple task, especially for those well-versed in mathematics. However, understanding the underlying principles and various methods for comparing fractions is crucial for a strong grasp of fundamental arithmetic. This article will not only answer the question definitively but will also explore multiple approaches to fraction comparison, providing a comprehensive understanding of the concept for students and adults alike.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the basics of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For instance, in the fraction 5/8, the numerator (5) indicates we have 5 parts, and the denominator (8) indicates the whole is divided into 8 equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once this is achieved, we can directly compare the numerators.
Let's apply this method to 5/8 and 1/2:
-
Find the least common multiple (LCM) of the denominators: The denominators are 8 and 2. The LCM of 8 and 2 is 8 (because 8 is a multiple of 2).
-
Convert the fractions to equivalent fractions with the common denominator:
- 5/8 already has a denominator of 8, so it remains unchanged.
- To convert 1/2 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
-
Compare the numerators: Now we compare 5/8 and 4/8. Since 5 > 4, we conclude that 5/8 > 1/2.
Method 2: Converting to Decimals
Another effective method involves converting fractions to decimals. This approach offers a more intuitive comparison, especially for those who find decimal comparisons easier.
-
Convert each fraction to a decimal:
- 5/8 = 0.625
- 1/2 = 0.5
-
Compare the decimals: Since 0.625 > 0.5, we again conclude that 5/8 > 1/2.
This method is particularly useful when dealing with more complex fractions or when a quick, approximate comparison is sufficient. However, it relies on the ability to perform accurate decimal conversions.
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially for younger learners or those who prefer a more concrete approach. Imagine a pizza cut into 8 slices (representing the denominator of 5/8). 5/8 represents 5 of those slices.
Now, imagine another pizza cut into 2 equal halves (representing the denominator of 1/2). 1/2 represents one of those halves. If you compare the portion of pizza represented by 5/8 to the portion represented by 1/2, it becomes visually clear that 5/8 is larger.
This method excels at building intuitive understanding, but it may be less practical for comparing complex fractions.
Method 4: Using a Number Line
A number line provides a visual representation of the relative positions of fractions. Plotting both fractions on a number line clearly demonstrates their order.
A number line ranging from 0 to 1 can be used. Mark the points 0, 1/2, and 1. Then, locate 5/8 between 1/2 and 1. The position of 5/8 will be to the right of 1/2, visually confirming that 5/8 > 1/2.
Exploring Further: Expanding on Fraction Comparison Techniques
The methods described above provide a solid foundation for comparing fractions. However, understanding the underlying mathematical principles allows for more advanced techniques and a deeper appreciation of the subject.
Understanding Equivalence and Simplification
Before comparing fractions, it's often beneficial to simplify them to their lowest terms. This involves dividing both the numerator and denominator by their greatest common divisor (GCD). While simplifying doesn't directly impact the comparison, it simplifies the calculations involved in other methods. For example, 4/8 simplifies to 1/2.
Comparing Fractions with Different Numerators and Denominators
When comparing fractions with vastly different numerators and denominators, converting to decimals or finding a common denominator can become cumbersome. In such scenarios, cross-multiplication provides a streamlined approach.
Cross-multiplication: To compare fractions a/b and c/d, we cross-multiply:
- a x d and b x c
- If a x d > b x c, then a/b > c/d.
- If a x d < b x c, then a/b < c/d.
- If a x d = b x c, then a/b = c/d.
Let's apply this to 5/8 and 1/2:
5 x 2 = 10 8 x 1 = 8
Since 10 > 8, 5/8 > 1/2.
This method bypasses the need for finding a common denominator or converting to decimals, streamlining the comparison process.
Practical Applications of Fraction Comparison
Understanding fraction comparison isn't just a theoretical exercise; it has numerous practical applications in everyday life and various fields:
-
Cooking and Baking: Recipes frequently involve fractions, and accurate comparisons are crucial for achieving the desired results. Adjusting recipe quantities requires a precise understanding of fraction relationships.
-
Construction and Engineering: Precise measurements and calculations are paramount in these fields. Fraction comparison is vital for ensuring accuracy and preventing errors.
-
Finance and Budgeting: Managing finances effectively involves working with fractions and percentages (which are essentially fractions). Understanding fraction relationships is crucial for budgeting, calculating interest rates, and understanding investment returns.
-
Data Analysis and Statistics: Many statistical calculations involve fractions and ratios. Correctly interpreting data relies heavily on accurate fraction comparison and understanding.
Conclusion: Mastering Fraction Comparison
Determining whether 5/8 or 1/2 is larger is a fundamental skill in mathematics. This article has explored several methods—finding a common denominator, converting to decimals, visual representation, using a number line, and cross-multiplication—highlighting the versatility and importance of mastering these techniques. The ability to confidently compare fractions is crucial for success in numerous academic and real-world applications. By understanding these various methods and their underlying principles, you'll not only solve simple comparisons like this but also tackle more complex fraction problems with greater ease and confidence. Remember, practice is key to solidifying your understanding and improving your speed and accuracy when working with fractions.
Latest Posts
Latest Posts
-
Look At This Building This Is An Example Of A
Mar 31, 2025
-
How Many Crackers Are In A Sleeve Of Saltines
Mar 31, 2025
-
Highest Common Factor Of 45 And 60
Mar 31, 2025
-
How Much Older Is Big Than Carrie
Mar 31, 2025
-
What Does Do It With No Hands Mean
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Which Is Larger 5 8 Or 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
