Which Number Produces An Irrational Number When Multiplied By
Arias News
Apr 01, 2025 · 5 min read
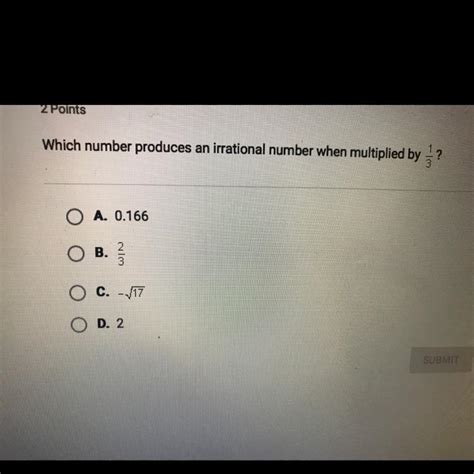
Table of Contents
Which Number Produces an Irrational Number When Multiplied By? Exploring the Nature of Irrational Numbers
The question of which number, when multiplied by another, yields an irrational number is surprisingly nuanced and leads us down a fascinating rabbit hole exploring the very nature of irrational numbers. Understanding this requires a grasp of both rational and irrational numbers, their properties, and the consequences of their interactions. Let's delve into this mathematical mystery.
Understanding Rational and Irrational Numbers
Before we tackle the central question, let's establish a firm foundation by defining our key players: rational and irrational numbers.
Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Examples include 1/2, -3, 0, and 0.75 (which can be expressed as 3/4). Essentially, rational numbers can be represented exactly as a ratio of two whole numbers. Their decimal representations either terminate (like 0.75) or repeat infinitely with a predictable pattern (like 1/3 = 0.333...).
Irrational numbers, on the other hand, cannot be expressed as a fraction of two integers. Their decimal representations are infinite and non-repeating. Famous examples include π (pi), approximately 3.14159..., and √2 (the square root of 2), approximately 1.41421... These numbers go on forever without ever settling into a repeating pattern.
The set of real numbers encompasses both rational and irrational numbers.
The Multiplicative Mystery: Creating Irrational Numbers
The core question revolves around finding a number that, when multiplied by another number, always results in an irrational number. This is a trickier problem than it initially seems. Let's explore some scenarios:
Scenario 1: Multiplying by an Irrational Number
If we multiply an irrational number by a non-zero rational number, the result is often (but not always) irrational. For instance:
- π * 2 = 2π This remains irrational.
- √2 * 3 = 3√2 This also stays irrational.
However, this isn't a guaranteed rule. Consider this exception:
- 0 * π = 0 Zero is a rational number.
Therefore, simply multiplying by an irrational number doesn't guarantee an irrational product.
Scenario 2: Multiplying by a Rational Number
If we multiply an irrational number by a rational number (excluding zero), the result is usually irrational. Let's examine why:
Assume we have an irrational number 'x' and a rational number 'r' (r ≠ 0). If their product 'rx' were rational (let's say p/q), then we could write:
rx = p/q
Solving for x:
x = p/(qr)
Since p, q, and r are rational, p/(qr) is also rational. This contradicts our initial assumption that x is irrational. Therefore, the product of a non-zero rational number and an irrational number is usually irrational. However, special cases arise, such as multiplying by zero.
Scenario 3: The Search for a Universal Multiplier
The question becomes: is there a single number that, when multiplied by any other number, guarantees an irrational product? The answer is no. There isn't a universal multiplier that transforms all numbers into irrational numbers. This is because:
-
Multiplying by Zero: As we've seen, multiplying any number by zero always results in zero, which is rational. This single exception eliminates the possibility of a universal irrational-producing multiplier.
-
Multiplicative Identity: Multiplying any number by 1 always yields the original number. Thus, if we start with a rational number, the product remains rational.
Deeper Exploration: Properties of Irrational Numbers and Algebraic Operations
The behavior of irrational numbers under various mathematical operations adds another layer of complexity to our investigation. Let's explore some key properties:
Addition and Subtraction
Adding or subtracting rational numbers always results in a rational number. However, adding or subtracting an irrational number to a rational number often produces an irrational number (with the exception of specific cases where they cancel each other out). For example:
- 2 + π = An irrational number
- 5 - √2 = An irrational number
Adding or subtracting two irrational numbers can result in either a rational or an irrational number. For example:
- √2 + (-√2) = 0 (rational)
- √2 + π = An irrational number
Multiplication and Division
As we've discussed, multiplying an irrational number by a non-zero rational number usually yields an irrational number, while multiplication by zero gives a rational result. The same principle applies to division, given that division is just multiplication by the reciprocal.
Transcendental Numbers and Algebraic Numbers
Within the realm of irrational numbers, there's a further classification into transcendental and algebraic numbers:
- Algebraic numbers are roots of polynomial equations with rational coefficients (e.g., √2 is a root of x² - 2 = 0).
- Transcendental numbers are not algebraic; they cannot be roots of such equations. Examples include π and e (Euler's number).
Understanding this distinction is crucial for exploring more advanced mathematical properties and the behavior of irrational numbers under different operations.
Practical Implications and Applications
Understanding the properties of rational and irrational numbers extends beyond pure mathematical curiosity. These concepts play a crucial role in various fields:
-
Geometry: The very nature of π, an irrational number, is fundamental in calculations involving circles, spheres, and other curved shapes.
-
Physics: Irrational numbers often appear in physical constants and equations describing natural phenomena.
-
Computer Science: Representing and working with irrational numbers within computer systems presents unique challenges, as they necessitate approximations.
-
Engineering: Precise calculations in engineering often require careful consideration of the precision needed when dealing with irrational numbers.
Conclusion: The Intricate World of Irrational Numbers
The question of which number produces an irrational number when multiplied by another highlights the richness and complexity of irrational numbers. While there isn't a single universal multiplier that guarantees an irrational product, the behavior of irrational numbers under different operations provides a fertile ground for mathematical exploration and discovery. The seemingly simple question opens a door to a deeper understanding of fundamental mathematical concepts and their application across various scientific disciplines. Further research into the properties of transcendental and algebraic numbers can lead to even more profound insights into this fascinating area of mathematics.
Latest Posts
Latest Posts
-
Dog Breed That Starts With An X
Apr 02, 2025
-
6 And 1 Half Dozen The Other
Apr 02, 2025
-
How Old Are You If Born In 1994
Apr 02, 2025
-
How Many Ounces Is 1 3 Gallon
Apr 02, 2025
-
How To Say You Are Ugly In Spanish
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Which Number Produces An Irrational Number When Multiplied By . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
