Which Of These Figures Has Rotational Symmetry
Arias News
Apr 01, 2025 · 6 min read
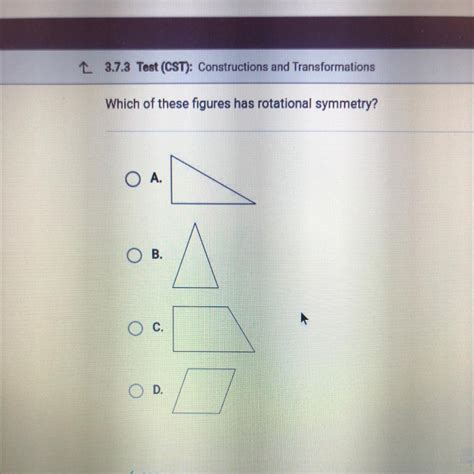
Table of Contents
Which of These Figures Has Rotational Symmetry? A Deep Dive into Geometric Transformations
Rotational symmetry, a fascinating concept in geometry, describes the property of a shape remaining unchanged after rotation about a fixed point. Understanding rotational symmetry requires grasping the core principles of rotations, angles of rotation, and order of rotational symmetry. This article will explore these concepts in detail, providing numerous examples and clarifying the distinction between rotational symmetry and other types of symmetry, like reflectional symmetry. We'll delve into various geometric shapes, helping you confidently identify which possess rotational symmetry and to what degree.
Understanding Rotational Symmetry
Rotational symmetry, also known as radial symmetry, occurs when a figure can be rotated around a central point (the center of rotation) by a certain angle, and the rotated figure appears identical to the original. This isn't just about turning the shape; it's about the shape maintaining its exact form and position throughout the rotation.
Key Elements of Rotational Symmetry:
-
Center of Rotation: This is the fixed point around which the rotation occurs. It's often (but not always) the geometric center of the figure.
-
Angle of Rotation: This is the amount the figure is rotated. The angle must be less than 360 degrees. If the shape is identical after a rotation of θ degrees, it will also be identical after a rotation of 2θ, 3θ, and so on, up to (n-1)θ, where 'n' is the order of rotational symmetry.
-
Order of Rotational Symmetry: This indicates how many times a figure can be rotated (less than 360°) and still look exactly the same. A figure with order 'n' has 'n' lines of symmetry passing through the center of rotation. A regular polygon with 'n' sides has an order of rotational symmetry 'n'.
Examples of Figures with Rotational Symmetry
Let's explore various figures and analyze their rotational symmetry:
1. Regular Polygons: The Quintessential Example
Regular polygons (shapes with equal sides and equal angles) are prime examples of figures with rotational symmetry. The order of rotational symmetry for a regular n-sided polygon is 'n'.
-
Equilateral Triangle (3 sides): Order of rotational symmetry is 3. It can be rotated 120° and 240° and still look the same.
-
Square (4 sides): Order of rotational symmetry is 4. It can be rotated 90°, 180°, and 270° and still look the same.
-
Regular Pentagon (5 sides): Order of rotational symmetry is 5. It can be rotated 72°, 144°, 216°, and 288° and still look the same.
-
Regular Hexagon (6 sides): Order of rotational symmetry is 6. It can be rotated 60°, 120°, 180°, 240°, and 300° and still look the same.
The pattern continues: a regular n-sided polygon has an order of rotational symmetry of n.
2. Circles: Infinite Rotational Symmetry
Circles possess infinite rotational symmetry. They can be rotated by any angle, and they will always look the same. There's no limit to the number of times you can rotate a circle and still have it appear identical.
3. Stars: A Complex Case
Stars, particularly regular stars, exhibit rotational symmetry, but determining the order can be slightly more complex. For example:
-
Pentagram (five-pointed star): The order of rotational symmetry is 5.
-
Hexagram (six-pointed star): The order of rotational symmetry is 6. Note that some six-pointed stars might have a different order depending on their construction.
The order of rotational symmetry in stars depends on the number of points and how they are interconnected.
4. Other Shapes with Rotational Symmetry
Many other shapes exhibit rotational symmetry:
-
Certain types of flowers: Many flowers have rotational symmetry, often with orders of 3, 4, 5, or more.
-
Snowflakes: Many snowflakes possess rotational symmetry, though not always perfect or of a high order.
-
Man-made objects: Logos, wheels, and many other designed objects are frequently created with rotational symmetry for aesthetic or functional reasons.
-
Some letters: Letters like "H", "I", "N", "O", "S", "X", and "Z" exhibit rotational symmetry of order 2 (180° rotation).
Differentiating Rotational Symmetry from Reflectional Symmetry
It's crucial to distinguish rotational symmetry from reflectional symmetry (also called line symmetry or bilateral symmetry). Reflectional symmetry occurs when a shape can be folded along a line (the line of symmetry) so that the two halves match exactly.
A figure can have:
-
Only rotational symmetry: For example, a non-regular pentagon might have rotational symmetry of order 1 (only a 360° rotation leaves it unchanged), but no reflectional symmetry.
-
Only reflectional symmetry: A scalene triangle, for example, has no rotational symmetry but may have one line of reflectional symmetry.
-
Both rotational and reflectional symmetry: Regular polygons possess both types of symmetry.
Practical Applications of Rotational Symmetry
Rotational symmetry is not just a mathematical concept; it has numerous practical applications:
-
Engineering and Design: Understanding rotational symmetry is crucial in designing wheels, gears, turbines, and other rotating machinery. The symmetrical nature ensures balanced performance and reduces vibrations.
-
Architecture: Many architectural designs incorporate rotational symmetry for aesthetic appeal and structural stability.
-
Art and Design: Artists and designers frequently use rotational symmetry in their work to create visually appealing and balanced compositions.
-
Nature: Rotational symmetry is prevalent in nature, appearing in flowers, snowflakes, and many other natural phenomena.
-
Logo Design: Many company logos utilize rotational symmetry to create memorable and easily recognizable symbols.
Identifying Rotational Symmetry: A Step-by-Step Guide
Here's a step-by-step process to determine if a figure possesses rotational symmetry:
-
Locate the Center of Rotation: Identify the point around which the figure might be rotated. This is often the geometric center, but not always.
-
Rotate the Figure: Mentally or physically rotate the figure by small increments (e.g., 15°, 30°, 45°, etc.).
-
Observe for Identity: After each rotation, check if the figure looks exactly the same as the original.
-
Determine the Order: Count the number of times the figure looks identical during a 360° rotation. This number is the order of rotational symmetry.
Conclusion: Mastering the Art of Rotational Symmetry
Understanding rotational symmetry requires careful consideration of angles of rotation, centers of rotation, and the order of symmetry. This article has explored the concept in depth, providing examples and differentiating it from other types of symmetry. By applying the steps outlined above, you can effectively identify and analyze rotational symmetry in various geometric shapes and objects, furthering your appreciation for this fundamental concept in geometry and its wide-ranging applications in various fields. From the elegance of regular polygons to the intricate patterns found in nature, rotational symmetry reveals a hidden order in the world around us.
Latest Posts
Latest Posts
-
Can You Work At Kroger At 14
Apr 02, 2025
-
How Long Does It Take To Drive Across Tennessee
Apr 02, 2025
-
How Far Is 14 Miles In Minutes
Apr 02, 2025
-
What Does Ditto Mean In A Text Message
Apr 02, 2025
-
How Many Pounds Are In 8 Tons
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Which Of These Figures Has Rotational Symmetry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
