30 Out Of 35 As A Percentage
Arias News
May 10, 2025 · 4 min read
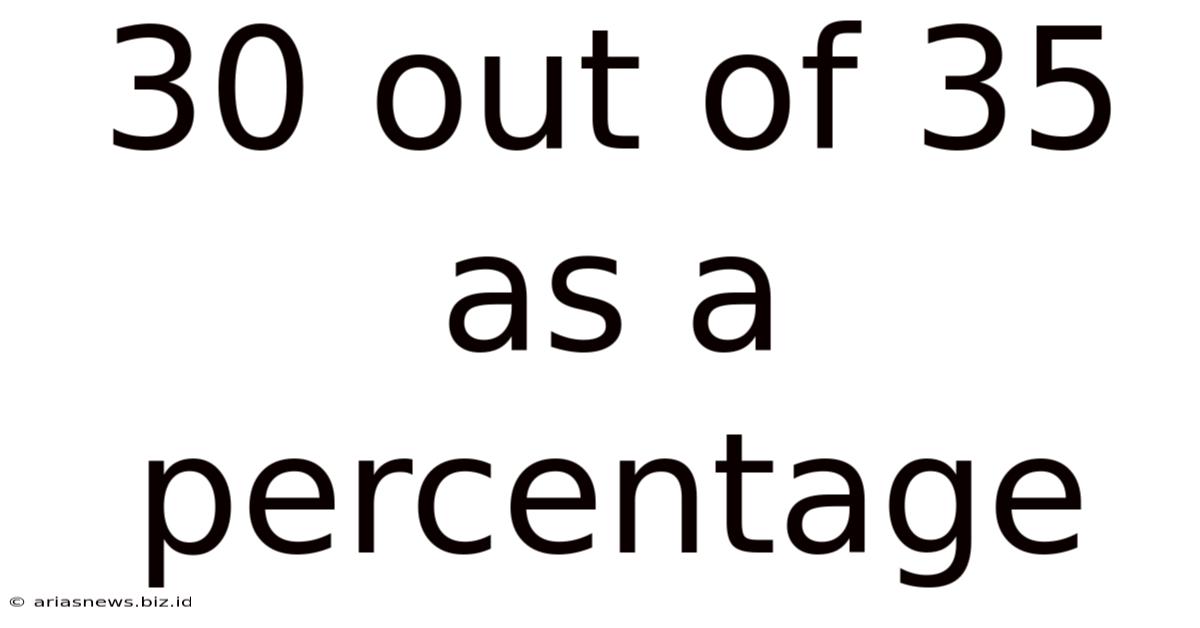
Table of Contents
30 out of 35 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis. Understanding how to express a portion of a whole as a percentage is crucial for interpreting data, making comparisons, and drawing informed conclusions. This article will delve into the calculation of "30 out of 35 as a percentage," providing a step-by-step guide, exploring different calculation methods, and offering real-world applications. We'll also cover related percentage calculations and address common misconceptions.
Understanding the Fundamentals of Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The symbol "%" signifies "per hundred" or "out of 100." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. This fundamental concept is the basis for all percentage calculations.
Calculating 30 out of 35 as a Percentage: The Simple Method
The most straightforward method involves converting the given fraction (30/35) into a decimal and then multiplying by 100 to express it as a percentage.
Step 1: Formulate the Fraction:
Represent "30 out of 35" as a fraction: 30/35
Step 2: Simplify the Fraction (Optional):
Simplifying fractions makes the subsequent calculations easier. Both 30 and 35 are divisible by 5:
30 ÷ 5 = 6 35 ÷ 5 = 7
Therefore, 30/35 simplifies to 6/7.
Step 3: Convert the Fraction to a Decimal:
Divide the numerator (6) by the denominator (7):
6 ÷ 7 ≈ 0.8571
Step 4: Convert the Decimal to a Percentage:
Multiply the decimal by 100 and add the percentage symbol (%):
0.8571 × 100 ≈ 85.71%
Therefore, 30 out of 35 is approximately 85.71%.
Alternative Calculation Method: Using Proportions
Another approach involves setting up a proportion. We can set up a proportion where x represents the percentage we want to find:
30/35 = x/100
To solve for x, we cross-multiply:
35x = 3000
Then, divide both sides by 35:
x = 3000/35 ≈ 85.71
Again, we arrive at the same result: approximately 85.71%.
Understanding Rounding in Percentage Calculations
In many cases, percentage calculations result in decimal values. Rounding is often necessary to express the percentage in a more manageable form. The level of rounding depends on the context. For example, in academic grading, rounding to the nearest whole number might be sufficient. In financial calculations, however, greater precision might be required. In our example, rounding 85.71% to the nearest whole number yields 86%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
- Academic Performance: Calculating grades based on scores achieved in tests or assignments.
- Financial Analysis: Determining profit margins, interest rates, discounts, and tax rates.
- Data Interpretation: Analyzing survey results, statistical data, and market research.
- Sports Statistics: Calculating batting averages, winning percentages, and player efficiency ratings.
- Everyday Life: Calculating tips, discounts in stores, and understanding sales promotions.
Calculating Related Percentages: Variations on the Theme
Once you understand the fundamental process, you can easily adapt it to calculate other percentages. For instance:
-
What is 35 out of 30 as a percentage? This results in a percentage greater than 100%, indicating that the first number is larger than the second. Following the same method, 35/30 ≈ 1.1667, which translates to approximately 116.67%.
-
What percentage is 5 out of 35? This is a smaller fraction, reflecting a lower percentage. 5/35 simplifies to 1/7. 1 ÷ 7 ≈ 0.1429, which is approximately 14.29%.
-
What percentage is 20 out of 35? Similar to the above examples, we find 20/35 simplifies to 4/7. 4 ÷ 7 ≈ 0.5714, leading to approximately 57.14%.
Common Misconceptions Regarding Percentage Calculations
Several common misconceptions can lead to errors in percentage calculations. These include:
- Confusing Fractions and Decimals: Failing to correctly convert between fractions and decimals before calculating percentages.
- Incorrect Rounding: Rounding numbers prematurely or inconsistently can lead to inaccurate results.
- Misinterpreting Percentages Greater than 100%: Percentages greater than 100% simply indicate that the numerator is greater than the denominator.
- Misunderstanding the Concept of Percentage Increase/Decrease: The calculation methods differ between calculating the percentage of a number and finding a percentage increase or decrease.
Advanced Percentage Calculations: Beyond the Basics
While the examples above cover basic percentage calculations, more complex scenarios exist. For example, understanding compound interest involves multiple percentage calculations over time. Likewise, calculating percentage changes requires a specific formula accounting for the initial and final values.
Conclusion: Mastering Percentage Calculations for Success
The ability to accurately calculate percentages is an invaluable skill across various aspects of life. Understanding the fundamental concepts, mastering the different calculation methods, and being aware of common pitfalls are crucial for accurate and efficient calculation. This article has provided a comprehensive guide to calculating percentages, including the specific calculation of "30 out of 35 as a percentage," along with various related examples and practical applications. By mastering these principles, you'll enhance your analytical abilities and improve your ability to interpret data effectively in both professional and personal settings. The more you practice, the more confident and accurate you'll become in your percentage calculations.
Latest Posts
Latest Posts
-
What Is The Answer To An Addition Problem Called
May 10, 2025
-
How Many Pieces Of Vinyl Siding In A Square
May 10, 2025
-
What Is The Gcf Of 28 And 70
May 10, 2025
-
What Is The Square Root Of 2 Squared
May 10, 2025
-
What Is The Gcf Of 12 And 15
May 10, 2025
Related Post
Thank you for visiting our website which covers about 30 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.