30 Tens - 3 Tens 3 Tenths
Arias News
May 09, 2025 · 4 min read
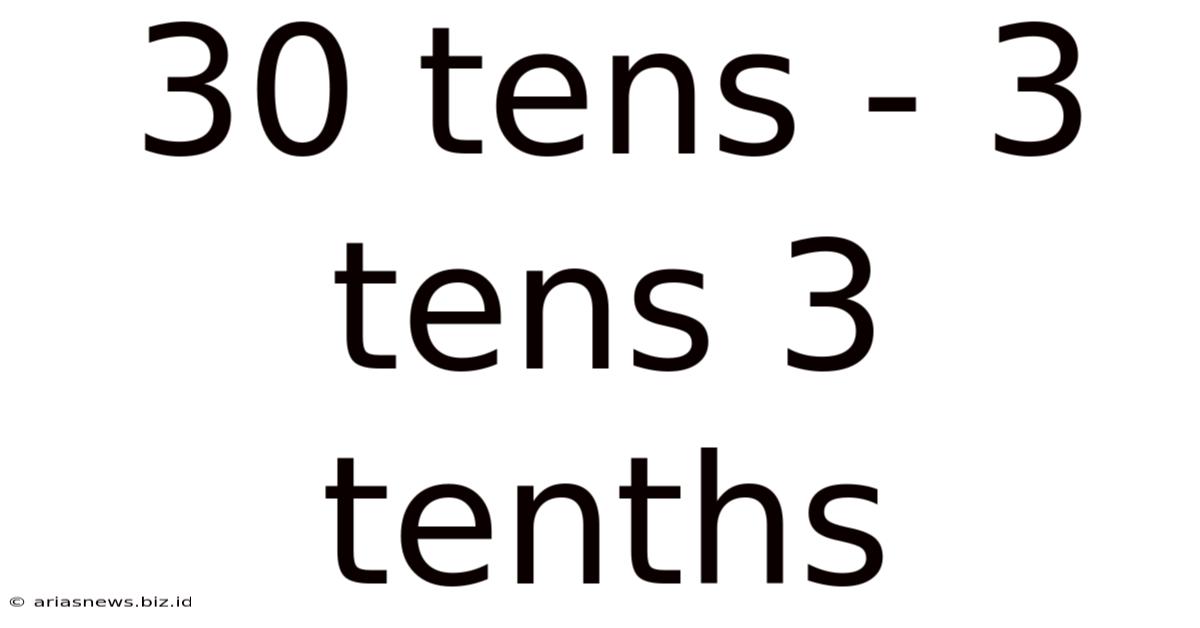
Table of Contents
30 Tens - 3 Tens 3 Tenths: A Deep Dive into Decimal Subtraction
Understanding decimal subtraction is crucial for various mathematical applications. This article delves into the problem "30 tens - 3 tens 3 tenths," breaking down the process step-by-step and exploring the underlying concepts. We'll cover different approaches to solving this problem, emphasizing the importance of place value understanding and providing examples to solidify your grasp of decimal subtraction. We'll also explore how this fundamental skill applies to real-world scenarios and advanced mathematical concepts.
Understanding the Problem: 30 Tens - 3 Tens 3 Tenths
The problem, "30 tens - 3 tens 3 tenths," presents a subtraction problem involving decimals. Let's first convert the numbers into a more familiar decimal format.
- 30 tens: This is equivalent to 300 (30 x 10 = 300).
- 3 tens 3 tenths: This translates to 30.3 (30 + 0.3 = 30.3).
Therefore, the problem becomes: 300 - 30.3.
Method 1: Standard Subtraction Algorithm
The most straightforward method involves using the standard subtraction algorithm, aligning the decimal points and borrowing when necessary.
299.10
- 30.30
-------
268.80
Step-by-step breakdown:
-
Align decimal points: Ensure the decimal points are vertically aligned. We add zeros to 300 (making it 300.00) to have the same number of decimal places.
-
Subtract from right to left: Starting from the hundredths place, we subtract 0 - 0 = 0.
-
Borrowing: In the tenths place, we encounter 0 - 3. Since we can't subtract a larger number from a smaller one, we borrow 1 from the ones place (making it 9). The borrowed 1 becomes 10 in the tenths place. Now, we have 10 - 3 = 7.
-
Continue borrowing: In the ones place, we have 9 - 0 = 9. In the tens place, we have 9 - 3 = 6. Finally, in the hundreds place, we have 2 - 0 = 2.
-
Result: The final result is 268.80 or 268.8
Method 2: Breaking Down the Subtraction
We can also break down the subtraction into smaller, more manageable steps. This method is beneficial for visualizing the process and reinforcing place value understanding.
- Subtract the tens: 30 tens - 3 tens = 27 tens = 270
- Subtract the tenths: 270 - 0.3 = 269.7
This method provides a slightly different approach but arrives at the same result.
Method 3: Using Number Lines (Visual Representation)
While less practical for large numbers, a number line can be a helpful visual aid, particularly for beginners. You can represent 300 and 30.3 on the number line and visually determine the difference. This method fosters a strong understanding of number relationships.
Understanding Place Value: The Key to Success
The success of any decimal subtraction hinges on a solid grasp of place value. Understanding that each place to the right of the decimal point represents a decreasing power of ten (tenths, hundredths, thousandths, etc.) is crucial. This understanding allows for accurate alignment of numbers and proper borrowing/carrying during calculations.
Real-World Applications
Decimal subtraction is not just an academic exercise; it's a vital skill used in everyday life:
-
Financial Calculations: Balancing your checkbook, calculating discounts, and determining the change you receive all involve decimal subtraction.
-
Measurement: Subtracting lengths, weights, or volumes often involves decimals. For example, calculating the remaining amount of paint after a project.
-
Scientific Calculations: Many scientific measurements involve decimal numbers, requiring precise subtraction for accurate results.
Extending the Concept: More Complex Decimal Subtraction
The principles applied to "30 tens - 3 tens 3 tenths" can be extended to more complex decimal subtraction problems. Remember the importance of:
-
Proper Alignment: Always align the decimal points before subtracting.
-
Borrowing: Understand and apply borrowing techniques effectively.
-
Place Value: Maintain a strong understanding of place value throughout the process.
Practicing Decimal Subtraction
Consistent practice is vital for mastering decimal subtraction. Start with simple problems and gradually increase the complexity. Using various methods, including standard algorithms and visual representations, can solidify your understanding. Online resources and workbooks can offer ample opportunities for practice.
Conclusion: Mastering Decimal Subtraction
Mastering decimal subtraction is essential for success in mathematics and various real-world applications. This article has provided a thorough explanation of the problem "30 tens - 3 tens 3 tenths," showcasing different solution methods and highlighting the importance of place value understanding. By understanding the underlying principles and practicing regularly, you can confidently tackle more complex decimal subtraction problems. Remember to always double-check your work and use different methods to ensure accuracy and deepen your understanding. The ability to perform accurate decimal subtraction is a cornerstone of numeracy and opens doors to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How Do You Say Hello Handsome In Spanish
May 09, 2025
-
How Long Is A 10 Mb Video
May 09, 2025
-
What Is 400 Km In Miles Per Hour
May 09, 2025
-
How Much Does A Cup Of Sugar Cost
May 09, 2025
-
Land Surrounded On Three Sides By Water
May 09, 2025
Related Post
Thank you for visiting our website which covers about 30 Tens - 3 Tens 3 Tenths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.