50 Out Of 70 As A Percentage
Arias News
May 09, 2025 · 5 min read
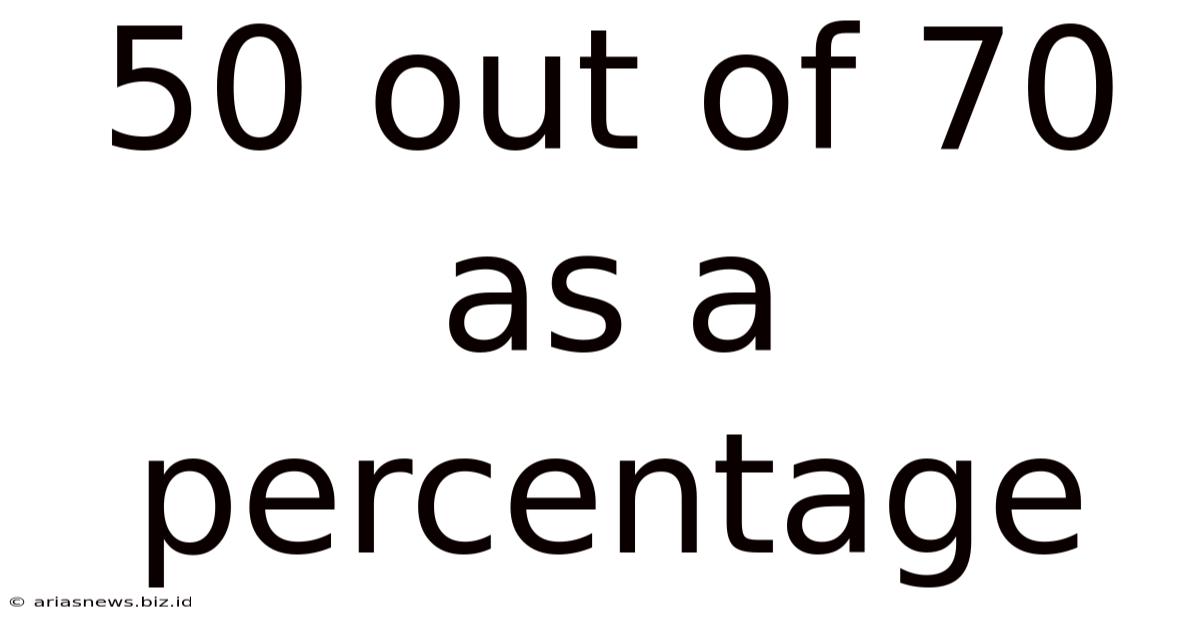
Table of Contents
50 out of 70 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial transactions and everyday life. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating numerical information effectively. This article delves into the calculation of 50 out of 70 as a percentage, providing a detailed explanation of the process and exploring related concepts to enhance your understanding of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of a hundred." Therefore, a percentage represents a proportion or ratio relative to a whole, which is considered 100%.
Calculating 50 out of 70 as a Percentage
To determine what percentage 50 represents out of 70, we employ a straightforward calculation:
-
Formulate the Fraction: Express the given numbers as a fraction. In this case, 50 is the part and 70 is the whole, resulting in the fraction 50/70.
-
Convert to Decimal: Divide the numerator (50) by the denominator (70): 50 ÷ 70 = 0.7142857...
-
Convert Decimal to Percentage: Multiply the decimal value by 100: 0.7142857... × 100 = 71.42857...%
-
Rounding: Round the percentage to the desired level of precision. Commonly, percentages are rounded to one or two decimal places. Rounding 71.42857...% to two decimal places yields 71.43%.
Therefore, 50 out of 70 is 71.43%.
Alternative Calculation Methods
While the method described above is the most straightforward, there are alternative approaches you can use:
Method 1: Using Proportions
This method involves setting up a proportion:
- x/100 = 50/70
Solving for 'x' gives you the percentage. Cross-multiply:
- 70x = 5000
Divide both sides by 70:
- x = 5000/70 = 71.43 (approximately)
Therefore, x = 71.43%
Method 2: Simplifying the Fraction First
Before performing the division, you can simplify the fraction 50/70 by finding the greatest common divisor (GCD) of 50 and 70, which is 10. Simplifying the fraction:
- 50/70 = (50 ÷ 10) / (70 ÷ 10) = 5/7
Now divide 5 by 7 and multiply by 100:
- (5 ÷ 7) × 100 = 0.7142857... × 100 ≈ 71.43%
This method can make the calculation slightly easier, especially with larger numbers.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world scenarios:
1. Academic Performance
Calculating grades, class averages, and individual progress often involves percentages. For example, if a student scores 50 out of 70 on a test, their percentage score is 71.43%, providing a clear representation of their performance.
2. Financial Matters
Percentages are widely used in finance, including calculating interest rates, discounts, tax rates, and profit margins. Understanding percentages helps in making informed financial decisions, such as comparing loan options or analyzing investment returns.
3. Sales and Marketing
Sales figures are often expressed as percentages of targets or previous periods. Marketing campaigns rely on percentage calculations to measure their effectiveness and return on investment (ROI).
4. Data Analysis and Statistics
Percentages are fundamental to data representation and interpretation. Graphs, charts, and statistical analyses often use percentages to visualize trends, patterns, and distributions.
5. Everyday Life
From calculating tips in restaurants to understanding sale discounts in stores, percentages are ubiquitous in our daily lives. A solid understanding of percentages makes these calculations effortless and efficient.
Common Percentage-Related Calculations
Beyond calculating a percentage from a fraction, several other related calculations are frequently encountered:
1. Finding a Percentage of a Number
To find a percentage of a number, multiply the number by the percentage (as a decimal). For example, to find 20% of 150:
- 150 × 0.20 = 30
2. Finding the Percentage Increase or Decrease
Percentage change is calculated as follows:
- Percentage Change = [(New Value - Old Value) / Old Value] × 100
For example, if a price increases from $100 to $120:
- Percentage Increase = [(120 - 100) / 100] × 100 = 20%
3. Finding the Original Value after a Percentage Change
If you know the new value and the percentage change, you can find the original value using the following formula:
- Original Value = New Value / (1 + Percentage Change/100) (for percentage increase)
- Original Value = New Value / (1 - Percentage Change/100) (for percentage decrease)
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Solve various problems to build your understanding and improve your speed.
-
Use Calculators Effectively: While mental calculations are beneficial, calculators can help with complex or time-consuming calculations, ensuring accuracy.
-
Understand the Concepts: Focus on grasping the underlying principles of percentages rather than just memorizing formulas. A solid conceptual foundation will make it easier to tackle more complex problems.
-
Check Your Work: Always double-check your calculations to avoid errors. Try using different methods to verify your answers.
-
Learn Shortcuts: Explore and practice shortcuts and mental math techniques to speed up your calculations.
Conclusion
Calculating 50 out of 70 as a percentage involves a simple yet powerful process that translates fractions into easily understandable proportions. Understanding this process and its application across various fields empowers you to interpret data, make informed decisions, and navigate everyday life more efficiently. This comprehensive guide provides a strong foundation for mastering percentage calculations and confidently applying this essential skill in any context. By utilizing the methods and tips outlined above, you can enhance your proficiency and build a strong understanding of percentages, a critical aspect of numeracy and problem-solving. Remember, continuous practice and understanding the underlying principles are key to achieving mastery.
Latest Posts
Latest Posts
-
How Do You Convert Grams Into Liters
May 09, 2025
-
1s2 2s2 2p5 Ion With 1 Charge
May 09, 2025
-
According To The Monk Why Does Fortune Abandon People
May 09, 2025
-
How Many Gallons Are In 21 Quarts
May 09, 2025
-
What Is My Grandmothers Brother To Me
May 09, 2025
Related Post
Thank you for visiting our website which covers about 50 Out Of 70 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.