66 And 2 3 As A Decimal
Arias News
Apr 04, 2025 · 5 min read
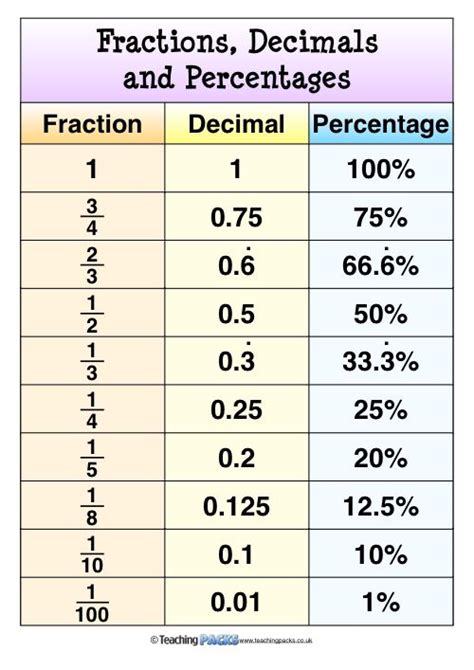
Table of Contents
66 and 2/3 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics with applications spanning various fields, from everyday calculations to complex scientific computations. This comprehensive guide delves into the process of converting the mixed number 66 and 2/3 into its decimal equivalent, exploring different methods and highlighting their practical implications. We'll also explore the broader context of fraction-to-decimal conversions and the importance of understanding this concept.
Understanding Fractions and Decimals
Before diving into the conversion, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For example, in the fraction 2/3, 2 is the numerator and 3 is the denominator. This means we have 2 parts out of a total of 3 parts.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, and so on). Decimals are expressed using a decimal point, separating the whole number part from the fractional part. For instance, 0.5 is equivalent to 1/2, 0.25 is equivalent to 1/4, and so on.
Converting 66 and 2/3 to a Decimal: Method 1 - Long Division
The most straightforward method for converting a fraction to a decimal is through long division. Since we have a mixed number (66 and 2/3), we first handle the whole number part and then convert the fractional part.
-
Separate the whole number: The whole number part of 66 and 2/3 is simply 66.
-
Convert the fraction: To convert the fraction 2/3 to a decimal, we perform long division: divide the numerator (2) by the denominator (3).
0.666... 3 | 2.000 -1 8 20 -18 20 -18 2...Notice that the division results in a repeating decimal: 0.666... The 6 repeats infinitely. This is often represented as 0.6̅.
-
Combine the whole number and decimal: Add the whole number part (66) to the decimal equivalent of the fraction (0.666...). This gives us 66.666... or 66.6̅.
Converting 66 and 2/3 to a Decimal: Method 2 - Using Equivalents
This method leverages the understanding that some fractions have readily available decimal equivalents. While not always directly applicable, understanding these equivalents can simplify conversions. Unfortunately, 2/3 doesn't have a simple, readily available decimal equivalent. Method 1 (long division) remains the most efficient approach in this specific case.
Understanding Repeating Decimals
The conversion of 66 and 2/3 resulted in a repeating decimal (66.6̅). Repeating decimals, also known as recurring decimals, are decimals with a digit or a group of digits that repeat infinitely. These are often denoted by placing a bar over the repeating digits. Understanding repeating decimals is crucial when working with fractions that cannot be expressed as a terminating decimal (a decimal that ends).
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is crucial in numerous real-world applications:
- Financial Calculations: Calculating percentages, interest rates, and other financial metrics often requires converting fractions to decimals.
- Engineering and Science: Measurements and calculations in various scientific and engineering fields frequently involve fractions that need to be expressed as decimals.
- Data Analysis: Data analysis often requires working with both fractions and decimals, so conversion is necessary for consistency and efficient analysis.
- Everyday Calculations: From baking to construction, understanding decimal equivalents is helpful for accurate measurements and calculations.
Rounding Decimals
In many practical applications, it's necessary to round repeating decimals to a certain number of decimal places. For example, 66.6̅ might be rounded to 66.7 (to one decimal place), 66.67 (to two decimal places), or 66.667 (to three decimal places). The choice of rounding depends on the required level of precision. The standard rules for rounding are applied: if the digit following the last significant digit is 5 or greater, round up; otherwise, round down.
Other Fraction-to-Decimal Conversions: Examples
Let's examine other fraction-to-decimal conversions to reinforce the concepts discussed:
- 1/4: Dividing 1 by 4 gives 0.25 (a terminating decimal).
- 3/8: Dividing 3 by 8 gives 0.375 (a terminating decimal).
- 1/3: Dividing 1 by 3 gives 0.333... or 0.3̅ (a repeating decimal).
- 5/6: Dividing 5 by 6 gives 0.8333... or 0.83̅ (a repeating decimal).
These examples illustrate that some fractions yield terminating decimals while others yield repeating decimals. The nature of the denominator determines whether the resulting decimal will terminate or repeat. Fractions with denominators that have only 2 and/or 5 as prime factors will always produce terminating decimals. Fractions with denominators containing prime factors other than 2 and 5 will always result in repeating decimals.
Advanced Concepts and Further Exploration
For those interested in delving deeper into the topic, further exploration could include:
- Binary and Hexadecimal Representations: Understanding how fractions are represented in different number systems.
- Continued Fractions: An alternative way to represent rational numbers that can be useful in certain mathematical contexts.
- Irrational Numbers: Exploring numbers that cannot be expressed as a fraction (e.g., π, √2). These numbers always have non-repeating, non-terminating decimal representations.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting fractions to decimals is a critical skill with widespread applicability. Understanding the different methods, especially long division, allows for accurate conversion of mixed numbers like 66 and 2/3 into their decimal equivalents (66.6̅). Recognizing the difference between terminating and repeating decimals and knowing how to handle rounding are essential components of mathematical fluency. The ability to confidently perform these conversions enhances problem-solving skills across various disciplines and everyday situations. By mastering these techniques, one gains a deeper understanding of numbers and their diverse representations.
Latest Posts
Latest Posts
-
Polygon With 5 Sides And 1 Right Angle
Apr 04, 2025
-
How Many Dots Are On A Pair Of Dice
Apr 04, 2025
-
How Many Fl Oz In 2 Gallons
Apr 04, 2025
-
Ice Cream Flavors That Start With H
Apr 04, 2025
-
How Many Ounces Is A Cup Of Broccoli
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 66 And 2 3 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
