Greatest Common Factor Of 48 And 64
Arias News
Apr 03, 2025 · 5 min read
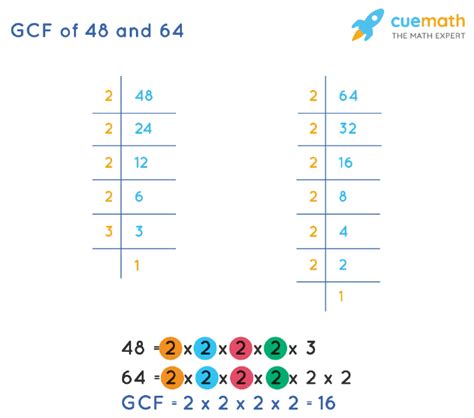
Table of Contents
Finding the Greatest Common Factor (GCF) of 48 and 64: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This comprehensive guide delves into various methods for determining the GCF of 48 and 64, providing a detailed explanation of each approach and highlighting its advantages and disadvantages. We'll explore prime factorization, the Euclidean algorithm, and the listing method, ensuring a thorough understanding of this crucial mathematical operation.
Understanding the Greatest Common Factor (GCF)
Before diving into the methods, let's define what the GCF actually is. The greatest common factor of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore the GCF of 12 and 18 is 6.
Our specific focus here is on finding the GCF of 48 and 64. This seemingly simple problem provides a perfect opportunity to illustrate several powerful techniques applicable to finding the GCF of any two numbers.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Then, we identify the common prime factors and multiply them together to find the GCF.
1. Prime Factorization of 48:
We can use a factor tree to find the prime factorization of 48.
48 = 2 x 24
= 2 x 2 x 12
= 2 x 2 x 2 x 6
= 2 x 2 x 2 x 2 x 3
= 2⁴ x 3¹
Therefore, the prime factorization of 48 is 2⁴ x 3¹.
2. Prime Factorization of 64:
Let's repeat the process for 64.
64 = 2 x 32
= 2 x 2 x 16
= 2 x 2 x 2 x 8
= 2 x 2 x 2 x 2 x 4
= 2 x 2 x 2 x 2 x 2 x 2
= 2⁶
The prime factorization of 64 is 2⁶.
3. Identifying Common Prime Factors:
Now, we compare the prime factorizations of 48 and 64:
48 = 2⁴ x 3¹ 64 = 2⁶
The only common prime factor is 2.
4. Calculating the GCF:
To find the GCF, we take the lowest power of the common prime factor:
GCF(48, 64) = 2⁴ = 16
Therefore, the greatest common factor of 48 and 64 is 16.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Steps:
-
Divide the larger number (64) by the smaller number (48):
64 ÷ 48 = 1 with a remainder of 16
-
Replace the larger number with the remainder (16):
Now we find the GCF of 48 and 16.
-
Repeat the process:
48 ÷ 16 = 3 with a remainder of 0
Since the remainder is 0, the GCF is the last non-zero remainder, which is 16.
Therefore, the Euclidean algorithm confirms that the GCF(48, 64) = 16. This method is highly efficient, especially when dealing with larger numbers where prime factorization can become cumbersome.
Method 3: Listing Factors
This method, while straightforward, can be less efficient for larger numbers. It involves listing all the factors of each number and identifying the largest common factor.
1. Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
2. Factors of 64: 1, 2, 4, 8, 16, 32, 64
3. Common Factors: 1, 2, 4, 8, 16
4. Greatest Common Factor: The largest common factor is 16.
Again, we find that the GCF(48, 64) = 16. While this method is easy to understand, it becomes impractical for larger numbers with numerous factors.
Choosing the Best Method
The optimal method for finding the GCF depends on the numbers involved.
-
Prime Factorization: Best suited for smaller numbers where the prime factorization is relatively easy to determine. It provides a good understanding of the underlying structure of the numbers.
-
Euclidean Algorithm: Highly efficient for larger numbers. Its iterative nature makes it computationally faster than listing factors.
-
Listing Factors: Simple and intuitive for very small numbers, but becomes inefficient for larger numbers with many factors.
Applications of GCF
The GCF has numerous applications in various areas of mathematics and beyond:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 48/64 can be simplified by dividing both numerator and denominator by their GCF (16), resulting in the simplified fraction 3/4.
-
Solving Algebraic Equations: The GCF plays a crucial role in factoring algebraic expressions, simplifying equations, and finding solutions.
-
Geometry and Measurement: The GCF is used in problems involving area, volume, and other geometric calculations where common divisors are essential.
-
Real-world Applications: GCF has practical applications in various fields, such as dividing objects evenly, scheduling tasks with common intervals, and optimizing resource allocation.
Conclusion: Mastering the GCF
Understanding and applying different methods for finding the greatest common factor is essential for proficiency in mathematics. Whether you choose prime factorization, the Euclidean algorithm, or the listing method, the key is to select the most efficient approach based on the numbers involved. This guide has provided a detailed explanation of each method, illustrating their application in finding the GCF of 48 and 64. Mastering these techniques will significantly enhance your mathematical skills and open doors to solving a wider range of problems across various disciplines. Remember to practice regularly to solidify your understanding and improve your speed and accuracy in calculating the GCF. The more you practice, the more intuitive these methods will become, allowing you to efficiently tackle even more complex mathematical challenges.
Latest Posts
Latest Posts
-
How Much Does A Baseball Hat Weigh
Apr 04, 2025
-
What Grade Is A 5 Out Of 10
Apr 04, 2025
-
66 And 2 3 As A Decimal
Apr 04, 2025
-
Which Rotel Is Hotter Original Or Mild
Apr 04, 2025
-
How Much Is A Half A Pint In Cups
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor Of 48 And 64 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
