Is 1 2 Bigger Than 5 8
Arias News
Mar 30, 2025 · 5 min read
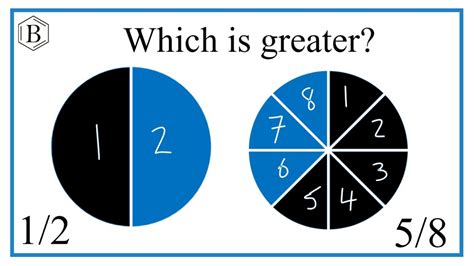
Table of Contents
Is 1/2 Bigger Than 5/8? A Deep Dive into Fraction Comparison
Determining whether one fraction is larger than another is a fundamental skill in mathematics. While seemingly simple, understanding the underlying principles behind fraction comparison is crucial for success in various mathematical fields and real-world applications. This comprehensive guide will explore the question, "Is 1/2 bigger than 5/8?", providing multiple methods to solve this problem and expanding on the broader topic of fraction comparison. We'll delve into conceptual understanding, practical techniques, and real-world examples to solidify your grasp of this essential mathematical concept.
Understanding Fractions: A Quick Recap
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) signifies that the whole is divided into two equal parts.
Method 1: Finding a Common Denominator
This is perhaps the most widely used method for comparing fractions. The core principle is to rewrite the fractions so they share the same denominator. This allows for a direct comparison of the numerators.
Steps:
-
Find the Least Common Multiple (LCM) of the denominators: The LCM is the smallest number that is a multiple of both denominators. For 1/2 and 5/8, the denominators are 2 and 8. The LCM of 2 and 8 is 8.
-
Convert the fractions to equivalent fractions with the LCM as the denominator:
-
For 1/2, we multiply both the numerator and the denominator by 4 (8/2 = 4): 1/2 * 4/4 = 4/8
-
5/8 already has a denominator of 8, so it remains unchanged.
-
-
Compare the numerators: Now we compare 4/8 and 5/8. Since 4 < 5, we conclude that 4/8 < 5/8.
Therefore, 1/2 is smaller than 5/8.
Method 2: Converting to Decimals
Another effective method involves converting the fractions into decimals. This allows for a straightforward numerical comparison.
Steps:
-
Divide the numerator by the denominator for each fraction:
-
1/2 = 1 ÷ 2 = 0.5
-
5/8 = 5 ÷ 8 = 0.625
-
-
Compare the decimal values: Since 0.5 < 0.625, we conclude that 1/2 < 5/8.
Therefore, 1/2 is smaller than 5/8.
Method 3: Visual Representation
Visual aids can be particularly helpful for understanding fraction comparison, especially for beginners.
Steps:
-
Draw a diagram representing the whole: You could use a circle, rectangle, or any shape.
-
Divide the whole into the number of parts indicated by the denominator: For 1/2, divide the shape into two equal parts. For 5/8, divide the shape into eight equal parts.
-
Shade the number of parts indicated by the numerator: Shade one part for 1/2 and five parts for 5/8.
-
Compare the shaded areas: Visually, it's clear that the shaded area representing 5/8 is larger than the shaded area representing 1/2.
Method 4: Using a Number Line
A number line provides a visual representation of the relative positions of fractions.
Steps:
-
Draw a number line from 0 to 1.
-
Divide the number line into equal segments based on the denominators: For 1/2 and 5/8, you might divide it into eighths (the LCM).
-
Plot the fractions on the number line: Locate 1/2 (which is equivalent to 4/8) and 5/8 on the number line.
-
Compare their positions: 5/8 will be to the right of 4/8 (or 1/2), indicating that 5/8 is larger.
Real-World Applications of Fraction Comparison
Understanding fraction comparison isn't just an abstract mathematical exercise. It has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often involve fractions. Knowing which fraction is larger is crucial for accurate measurements. For instance, determining whether you need 1/2 cup or 5/8 cup of sugar.
-
Measurement and Construction: In construction and engineering, precise measurements are essential. Comparing fractions is critical for ensuring accuracy in projects.
-
Finance and Budgeting: Understanding fractions is vital for managing finances. For instance, comparing fractions representing portions of a budget or understanding interest rates.
-
Data Analysis: In various fields, data analysis involves working with fractions and percentages, requiring a solid understanding of fraction comparison.
-
Time Management: Understanding fractions is helpful in time management. For instance, comparing the fraction of a day spent on different activities.
Beyond 1/2 and 5/8: Comparing Any Two Fractions
The methods discussed above – finding a common denominator, converting to decimals, using visual representations, and utilizing a number line – are applicable for comparing any two fractions, regardless of their numerators and denominators. The key is to choose the method that best suits your understanding and the specific problem at hand. For more complex fractions, converting to decimals or using a calculator can be particularly useful.
Expanding Your Fraction Skills: Further Exploration
Mastering fraction comparison is a stepping stone to more advanced mathematical concepts. To build upon your understanding, consider exploring the following:
-
Improper Fractions and Mixed Numbers: Learn how to convert between improper fractions (where the numerator is larger than the denominator) and mixed numbers (a combination of a whole number and a fraction).
-
Adding, Subtracting, Multiplying, and Dividing Fractions: Practice the four basic arithmetic operations with fractions.
-
Fraction to Decimal and Percentage Conversions: Fluently convert between fractions, decimals, and percentages.
-
Working with Fractions in Word Problems: Apply your knowledge of fraction comparison and operations to solve real-world problems.
Conclusion: Mastering the Art of Fraction Comparison
Determining whether 1/2 is bigger than 5/8 is a seemingly simple question, yet it opens the door to a deeper understanding of fractions and their applications. By mastering the techniques outlined in this guide – finding a common denominator, converting to decimals, visualizing fractions, and using a number line – you'll not only answer this specific question but also develop a solid foundation in fraction comparison, empowering you to tackle more complex mathematical challenges in your academic and professional pursuits. Remember, the key is to practice consistently and to choose the method that works best for you. With enough practice, comparing fractions will become second nature.
Latest Posts
Latest Posts
-
Price Per Pound To Price Per Kg
Apr 01, 2025
-
Greatest Common Factor Of 12 And 16
Apr 01, 2025
-
What Is 5 To The 5th Power
Apr 01, 2025
-
What Year Were You Born If You Are 19
Apr 01, 2025
-
How Do You Say Gravy In Spanish
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Bigger Than 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
