Is 1 2 Greater Than 2 4
Arias News
Apr 13, 2025 · 5 min read
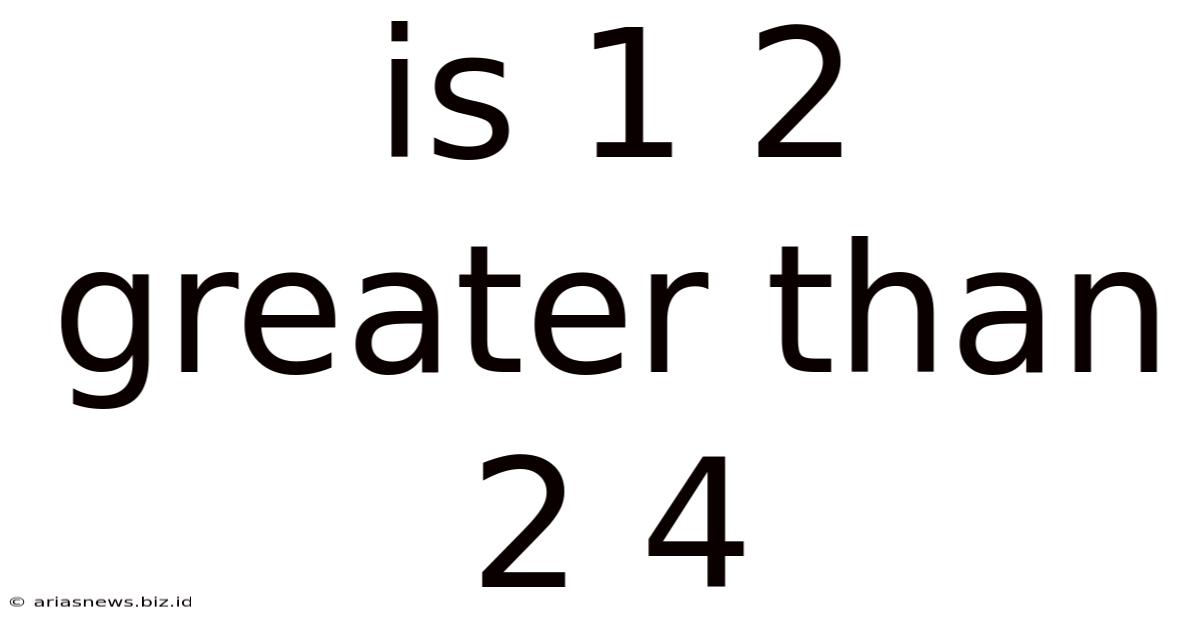
Table of Contents
Is 1/2 Greater Than 2/4? A Deep Dive into Fractions and Equivalence
The question, "Is 1/2 greater than 2/4?" might seem trivial at first glance. For many, the answer is immediately apparent. However, exploring this seemingly simple comparison offers a fantastic opportunity to delve into the fundamental concepts of fractions, equivalence, and their practical applications. This comprehensive guide will not only answer the question definitively but also equip you with a solid understanding of how to compare and manipulate fractions effectively.
Understanding Fractions: The Building Blocks
Before tackling the core question, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) signifies that the whole is divided into two equal parts.
Visualizing Fractions
Visual aids are incredibly helpful in grasping the concept of fractions. Imagine a pizza cut into two equal slices. If you take one slice, you have 1/2 of the pizza. Now, imagine the same pizza cut into four equal slices. Taking two slices gives you 2/4 of the pizza. This visual representation immediately highlights the equivalence between 1/2 and 2/4.
Equivalent Fractions: The Same Value, Different Representation
Equivalent fractions represent the same value, even though their numerators and denominators differ. They are essentially different ways of expressing the same proportion or part of a whole. We can obtain equivalent fractions by multiplying or dividing both the numerator and denominator by the same non-zero number.
This principle is crucial for comparing fractions. Often, comparing fractions with different denominators directly can be challenging. However, by converting them into equivalent fractions with a common denominator, the comparison becomes straightforward.
Finding Equivalent Fractions: A Step-by-Step Guide
To find an equivalent fraction, follow these steps:
- Choose a multiplier: Select a non-zero number to multiply both the numerator and denominator.
- Multiply the numerator: Multiply the original numerator by the chosen multiplier.
- Multiply the denominator: Multiply the original denominator by the same multiplier.
For instance, let's find an equivalent fraction for 1/2 using a multiplier of 2:
- Multiply the numerator: 1 x 2 = 2
- Multiply the denominator: 2 x 2 = 4
This gives us the equivalent fraction 2/4.
Comparing Fractions: Methods and Strategies
Several methods facilitate comparing fractions:
Method 1: Finding a Common Denominator
This is the most common and reliable method for comparing fractions. It involves converting the fractions into equivalent fractions with the same denominator. Then, you simply compare the numerators. The fraction with the larger numerator is the larger fraction.
Let's compare 1/2 and 2/4 using this method. We already know that 2/4 is an equivalent fraction of 1/2. Since their numerators (1 and 2) are equivalent, when converted to a common denominator, we can establish they have the same value.
Method 2: Converting to Decimals
Another approach involves converting the fractions into decimals. This is done by dividing the numerator by the denominator. Once you have the decimal equivalents, comparing the decimals becomes trivial.
For example:
- 1/2 = 0.5
- 2/4 = 0.5
Both fractions convert to 0.5, confirming their equality.
Method 3: Cross-Multiplication (for comparing two fractions)
Cross-multiplication is a quick method for comparing two fractions. Multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa. Compare the two products. The fraction corresponding to the larger product is the larger fraction.
Let's compare 1/2 and 2/4:
- 1 x 4 = 4
- 2 x 2 = 4
Since the products are equal, the fractions are equal.
The Verdict: 1/2 and 2/4
Applying any of the methods discussed above, we unequivocally conclude that 1/2 is equal to 2/4, not greater than it. They are equivalent fractions representing the same proportion or value.
Beyond the Basics: Real-World Applications
The concepts of fractions and equivalent fractions are far from abstract mathematical exercises. They have numerous practical applications in everyday life:
- Cooking and Baking: Recipes often use fractions to specify ingredient quantities. Understanding equivalent fractions allows for adjustments to recipe sizes.
- Measurement: Measuring length, volume, or weight frequently involves fractions. The ability to compare and convert fractions is essential for accurate measurements.
- Finance: Percentages, expressed as fractions (e.g., 10% = 1/10), are fundamental in finance for calculating interest, discounts, and taxes.
- Construction and Engineering: Precise calculations in construction and engineering rely heavily on fractions and their manipulation.
Mastering Fractions: Practice and Resources
Consistent practice is key to mastering fractions. Start with simple comparisons and gradually work your way towards more complex problems. Numerous online resources and workbooks provide practice exercises and tutorials on fractions.
Remember, understanding fractions is a foundational skill that permeates various aspects of life. By grasping the concepts of equivalence, comparison, and their applications, you'll build a stronger foundation in mathematics and improve your ability to solve real-world problems efficiently.
Conclusion: The Importance of Fractional Understanding
The seemingly simple question, "Is 1/2 greater than 2/4?" serves as a springboard for a deeper understanding of fractions, their equivalence, and their practical importance. By exploring different methods for comparing fractions and delving into their real-world applications, we highlight the significance of this foundational mathematical concept. Mastering fractions isn't just about passing tests; it's about equipping yourself with a crucial tool for navigating various aspects of life with greater accuracy and confidence. The ability to understand and manipulate fractions is a testament to one's numerical fluency and problem-solving capabilities. So, embrace the challenge, practice regularly, and enjoy the journey of mastering this essential mathematical skill.
Latest Posts
Latest Posts
-
Data In Order From The Smallest To Largest Or Vice Versa
May 09, 2025
-
Which Is Bigger 3 8 Or 5 8
May 09, 2025
-
What Does Bella Mia Mean In Italian
May 09, 2025
-
How Many Pounds Of Shredded Chicken Per Person
May 09, 2025
-
Half Of A Pint Equals How Many Cups
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Greater Than 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.