Which Is Bigger 3 8 Or 5 8
Arias News
May 09, 2025 · 5 min read
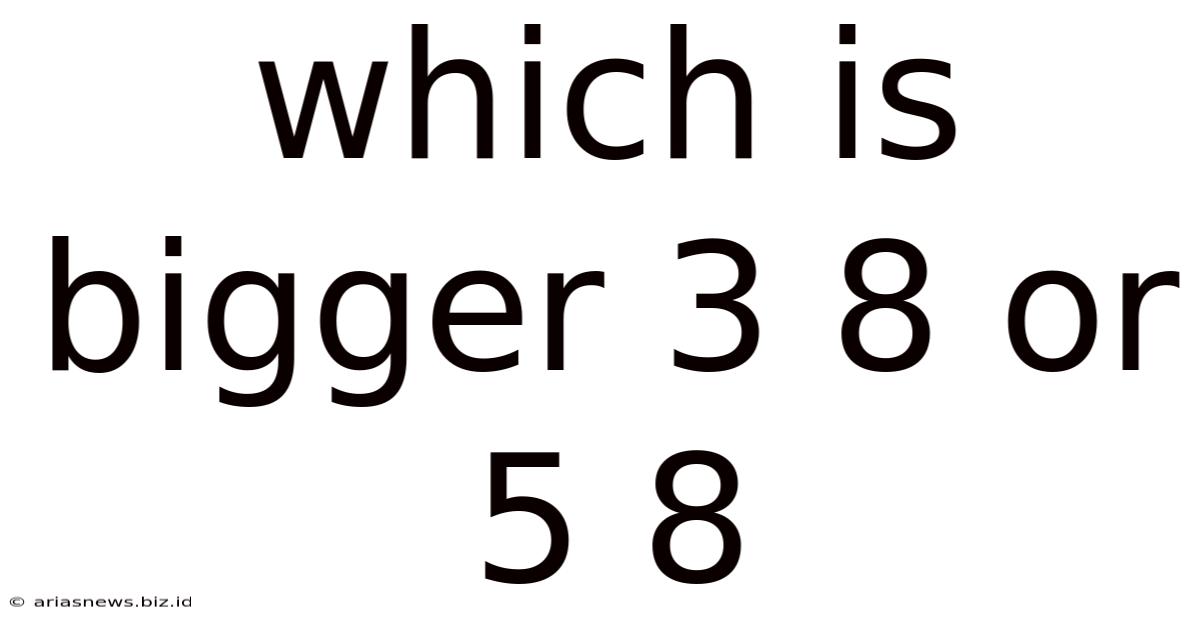
Table of Contents
Which is Bigger: 3/8 or 5/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in daily life and advanced studies. This article explores the seemingly simple question, "Which is bigger: 3/8 or 5/8?", delving into multiple methods for comparison, explaining the underlying principles, and extending the concept to more complex fractional comparisons. We'll also discuss practical applications and common misconceptions.
Visualizing Fractions: The Pizza Analogy
One of the easiest ways to grasp the concept of fraction comparison is through visualization. Imagine a pizza cut into eight equal slices.
- 3/8: This represents three slices out of the eight total slices.
- 5/8: This represents five slices out of the eight total slices.
Clearly, five slices are more than three slices. Therefore, 5/8 is bigger than 3/8.
This simple analogy provides a powerful visual representation that makes the comparison intuitive and easy to understand, particularly for beginners.
Numerical Comparison: Understanding Numerators and Denominators
Fractions consist of two key components:
- Numerator: The top number (e.g., 3 in 3/8 and 5 in 5/8) indicates the number of parts you have.
- Denominator: The bottom number (e.g., 8 in both fractions) indicates the total number of equal parts the whole is divided into.
When comparing fractions with the same denominator, as in this case (both are eighths), the fraction with the larger numerator is the larger fraction. Since 5 > 3, 5/8 > 3/8.
This rule simplifies the comparison significantly. It’s crucial to remember that this method only works when the denominators are identical.
The Importance of a Common Denominator: Extending the Comparison
When comparing fractions with different denominators, the process becomes slightly more complex. We need to find a common denominator, which is a number that is a multiple of both denominators. Let's illustrate with an example:
Compare 2/3 and 3/4.
To find a common denominator, we can use the least common multiple (LCM) of the denominators (3 and 4). The LCM of 3 and 4 is 12. We then convert each fraction to an equivalent fraction with a denominator of 12:
- 2/3 = (2 * 4) / (3 * 4) = 8/12
- 3/4 = (3 * 3) / (4 * 3) = 9/12
Now, we can easily compare 8/12 and 9/12. Since 9 > 8, 3/4 > 2/3.
This method of finding a common denominator is a cornerstone of fraction comparison and is applicable to any pair of fractions, regardless of their complexity.
Decimal Conversion: A Different Perspective
Another approach to comparing fractions is converting them to decimals. To do this, we simply divide the numerator by the denominator:
- 3/8 = 3 ÷ 8 = 0.375
- 5/8 = 5 ÷ 8 = 0.625
Comparing 0.375 and 0.625, we see that 0.625 > 0.375, confirming that 5/8 > 3/8.
Decimal conversion is particularly useful when dealing with fractions that are difficult to visualize or compare using common denominators. It provides a numerical representation that's easy to interpret.
Beyond Simple Comparisons: Advanced Fraction Techniques
The principles discussed above can be extended to more complex scenarios involving multiple fractions, mixed numbers (whole numbers and fractions), and even comparing fractions with negative values.
Comparing Mixed Numbers
A mixed number consists of a whole number and a fraction (e.g., 2 1/2). To compare mixed numbers, we can convert them to improper fractions (where the numerator is greater than or equal to the denominator). For example:
Compare 1 3/8 and 1 5/8.
- 1 3/8 = (1 * 8 + 3) / 8 = 11/8
- 1 5/8 = (1 * 8 + 5) / 8 = 13/8
Since 13 > 11, 1 5/8 > 1 3/8.
Alternatively, we can compare the whole number parts first. If they are different, the fraction with the larger whole number is larger. If the whole numbers are the same, compare the fractional parts as demonstrated previously.
Comparing Fractions with Different Denominators and Numerators: A Step-by-Step Guide
Let's compare 7/12 and 5/9.
- Find the Least Common Multiple (LCM): The LCM of 12 and 9 is 36.
- Convert to Equivalent Fractions:
- 7/12 = (7 * 3) / (12 * 3) = 21/36
- 5/9 = (5 * 4) / (9 * 4) = 20/36
- Compare: Since 21 > 20, 7/12 > 5/9.
This methodical approach ensures accuracy and helps build a strong foundation for handling more complex fractional comparisons.
Incorporating Negative Fractions
When comparing negative fractions, the order is reversed. The fraction closer to zero (the less negative fraction) is considered larger. For instance:
-3/8 and -5/8
Since -3 is greater than -5, -3/8 > -5/8. Remember, in negative numbers, the magnitude dictates the size, but the sign reverses the order of comparison.
Real-World Applications of Fraction Comparison
The ability to compare fractions is vital in numerous real-world scenarios:
- Cooking and Baking: Following recipes often involves working with fractions of ingredients. Understanding which fraction is larger ensures accurate measurements.
- Construction and Engineering: Precise measurements are critical, and comparing fractions is essential for accuracy and structural integrity.
- Finance and Budgeting: Managing finances frequently involves working with fractions of money. Comparing fractions helps determine which investment or expense is larger or smaller.
- Data Analysis: In data analysis, fractions often represent proportions or percentages. The ability to compare fractions allows for effective interpretation of data.
Common Misconceptions about Fraction Comparison
- Focusing solely on numerators: Many students initially make the mistake of comparing only the numerators, ignoring the denominators. This leads to incorrect conclusions. Always ensure the denominators are the same before comparing numerators.
- Incorrect LCM Calculation: Errors in calculating the least common multiple can lead to incorrect comparisons. Double-check your LCM calculations to avoid mistakes.
- Ignoring negative signs: The behavior of negative fractions differs from positive fractions. Remember to account for the negative signs when making comparisons.
Conclusion: Mastering Fraction Comparison
Comparing fractions, while seemingly simple at first glance, is a critical mathematical skill that extends far beyond simple exercises. Through visualization, numerical comparison, decimal conversion, and understanding common denominators, we can confidently compare fractions of any complexity. By mastering these techniques, we equip ourselves with the tools necessary to navigate a wide range of real-world situations and confidently tackle more advanced mathematical concepts. The ability to accurately compare fractions is a foundation for success in numerous academic and practical applications. Remember to practice regularly to solidify your understanding and build your confidence. The more you practice, the more intuitive fraction comparison will become.
Latest Posts
Latest Posts
-
How Much Does An Empty 53 Foot Trailer Weight
May 11, 2025
-
What Is One Half As A Percentage
May 11, 2025
-
What Is The Greatest Common Factor Of 7 And 21
May 11, 2025
-
What Color Shoes With A Lilac Dress
May 11, 2025
-
How Much Does 1 Gallon Of Fuel Weigh
May 11, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 3 8 Or 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.