Round 9.6 To The Nearest Whole Number.
Arias News
Mar 27, 2025 · 5 min read
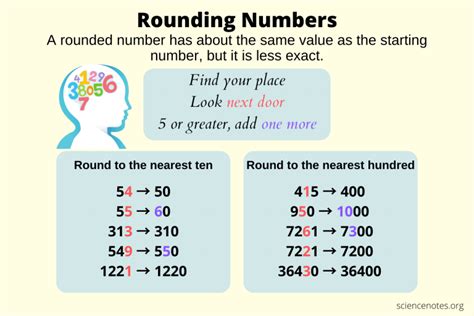
Table of Contents
Rounding 9.6 to the Nearest Whole Number: A Comprehensive Guide
Rounding numbers is a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating grocery bills to understanding complex scientific data. This comprehensive guide delves into the process of rounding 9.6 to the nearest whole number, explaining the underlying principles and providing various examples to solidify your understanding. We'll also explore the broader context of rounding, its significance in different fields, and common pitfalls to avoid.
Understanding the Concept of Rounding
Rounding involves approximating a number to a specified level of precision. This is crucial when dealing with numbers containing decimal places, where the exact value may not be necessary or practical. The process simplifies calculations and makes numbers easier to comprehend and use. The goal is to find the closest whole number, or integer, to the given number.
The key element in rounding is the digit immediately to the right of the place value you're rounding to. This is often referred to as the "rounding digit."
- If the rounding digit is 5 or greater (5, 6, 7, 8, or 9), we round up. This means we increase the digit to the left of the rounding digit by one.
- If the rounding digit is less than 5 (0, 1, 2, 3, or 4), we round down. This means we keep the digit to the left of the rounding digit the same.
Rounding 9.6 to the Nearest Whole Number: A Step-by-Step Approach
Let's apply these rules to round 9.6 to the nearest whole number.
-
Identify the place value: We are rounding to the nearest whole number, which means we're looking at the ones place.
-
Identify the rounding digit: The digit immediately to the right of the ones place is 6 (the tenths place).
-
Apply the rounding rule: Since the rounding digit (6) is greater than or equal to 5, we round up.
-
Perform the rounding: We increase the digit in the ones place (9) by one, resulting in 10.
Therefore, 9.6 rounded to the nearest whole number is 10.
Practical Applications of Rounding
Rounding is not merely an academic exercise; it has significant real-world applications across numerous fields:
1. Everyday Calculations:
- Shopping: When calculating the total cost of groceries, we often round prices to the nearest dollar to get a quick estimate.
- Tip Calculation: Rounding restaurant bills allows for quick and easy tip calculations.
- Budgeting: Rounding expenses helps in creating a simplified budget overview.
2. Scientific and Engineering Applications:
- Measurement: Measurements often involve approximations due to limitations in measuring instruments. Rounding helps present data in a more manageable format.
- Data Analysis: Large datasets often require rounding to simplify analysis and visualization.
- Statistical Calculations: Rounding is frequently used in statistical calculations to present results in a concise manner.
3. Financial Applications:
- Currency Exchange: Currency exchange rates are often rounded to a certain number of decimal places.
- Interest Calculations: Interest calculations frequently involve rounding to simplify computations.
- Stock Prices: Stock prices are typically displayed rounded to the nearest cent or even dollar.
4. Computer Science:
- Floating-Point Arithmetic: Computers use floating-point arithmetic, which inherently involves rounding due to limitations in representing real numbers.
- Data Storage: Rounding is used to efficiently store numerical data with reduced precision.
Understanding Significant Figures and Rounding
The concept of significant figures is closely related to rounding. Significant figures represent the number of digits in a number that carry meaning contributing to its precision. When rounding, we often aim to maintain a certain number of significant figures to ensure the accuracy of our calculations.
For instance, if we are working with measurements and need to maintain three significant figures, rounding 9.556 to three significant figures would give us 9.56. This contrasts with the simple rounding to the nearest whole number, where the result would be 10.
Common Mistakes in Rounding
While rounding seems straightforward, several common mistakes can lead to inaccuracies:
- Incorrect identification of the rounding digit: Failing to identify the correct digit to the right of the place value being rounded can lead to incorrect results.
- Incorrect application of rounding rules: Misunderstanding or misapplying the rules of rounding (rounding up when less than 5, or rounding down when 5 or greater) results in errors.
- Cascading rounding errors: When rounding multiple times in a sequence of calculations, errors can accumulate, leading to significant deviations from the true value. This is especially important in complex calculations.
- Not considering the context: Failing to consider the context of the rounding, such as the required precision or the number of significant figures, can lead to inappropriate levels of approximation.
Advanced Rounding Techniques
Beyond the basic rules, there are more sophisticated rounding methods:
- Rounding to a specific number of decimal places: This involves rounding to the nearest tenth, hundredth, thousandth, etc.
- Rounding to significant figures: This ensures that the result has a specific number of meaningful digits.
- Rounding half-up: In this method, numbers exactly halfway between two rounding values are always rounded up.
- Rounding half-down: Numbers exactly halfway between two rounding values are always rounded down.
- Rounding half-to-even (banker's rounding): Numbers exactly halfway are rounded to the nearest even number. This method minimizes bias over many rounding operations.
Conclusion: The Importance of Precision and Context in Rounding
Rounding is a critical skill in mathematics and various fields. Understanding the principles, applying the rules correctly, and considering the context are essential for accurate calculations and data representation. While the process of rounding 9.6 to the nearest whole number might seem simple, mastering the nuances ensures precision and reliability in numerical work. Remember to always consider the level of accuracy required and avoid common mistakes to ensure your calculations remain accurate and meaningful. The choice of rounding method often depends on the specific application and the desired level of precision. By understanding these different methods and their implications, you can confidently tackle various rounding challenges and improve your mathematical proficiency.
Latest Posts
Latest Posts
-
How Long Does It Take To Drive 80 Miles
Mar 30, 2025
-
How Many Feet Are In 156 Inches
Mar 30, 2025
-
What Is The Decimal For 2 1 2
Mar 30, 2025
-
When A Man Says He Loves You
Mar 30, 2025
-
How Many Pounds Is 1 2 Ton
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Round 9.6 To The Nearest Whole Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
