The Answer To An Addition Problem Is Called The
Arias News
Mar 26, 2025 · 6 min read
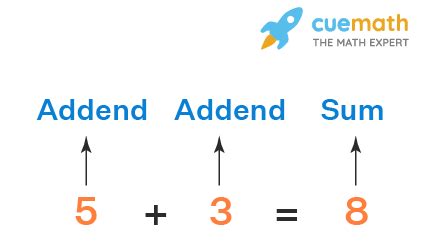
Table of Contents
The Answer to an Addition Problem is Called the Sum: A Deep Dive into Addition and its Properties
The seemingly simple question, "The answer to an addition problem is called the...?" has a straightforward answer: the sum. However, behind this simple term lies a rich world of mathematical concepts, properties, and applications that extend far beyond basic arithmetic. This article delves into the fascinating world of addition, exploring its fundamental principles, practical applications, and the significance of the sum within broader mathematical contexts. We'll cover everything from the basics of addition to advanced concepts relevant for students and enthusiasts alike.
Understanding Addition: The Foundation of Arithmetic
Addition, at its core, is the process of combining two or more quantities to find their total. It's a fundamental operation in arithmetic, forming the bedrock upon which more complex mathematical concepts are built. We use addition daily, from calculating the total cost of groceries to determining the combined distance of a journey. The components of an addition problem are crucial to understanding the concept of the sum:
Key Components of Addition
- Addends: These are the numbers being added together. In the equation 2 + 3 = 5, 2 and 3 are the addends. You can have two addends, three addends, or even more!
- Sum (or Total): This is the result of adding the addends together. In the equation 2 + 3 = 5, 5 is the sum. This is the answer to the addition problem.
- Plus Sign (+): This symbol indicates the operation of addition. It separates the addends and signifies that they are to be combined.
- Equals Sign (=): This symbol shows that the values on either side of it are equivalent. It signifies that the sum is equal to the result of adding the addends.
Properties of Addition: Unlocking Efficiency and Understanding
Addition isn't simply a mechanical process; it possesses several key properties that streamline calculations and offer deeper insights into its nature. Understanding these properties is vital for solving complex problems and grasping more advanced mathematical concepts:
1. Commutative Property: Order Doesn't Matter
The commutative property states that the order of the addends doesn't affect the sum. This means that 2 + 3 is the same as 3 + 2; both equal 5. This property simplifies calculations, allowing us to rearrange addends to make addition easier. For example, when adding a long list of numbers, it's often easier to group compatible numbers together (like grouping tens together).
2. Associative Property: Grouping Addends
The associative property allows us to group addends in different ways without changing the sum. For example, (2 + 3) + 4 is the same as 2 + (3 + 4). Both result in 9. This property is particularly useful when dealing with multiple addends, allowing for strategic grouping to simplify calculations.
3. Identity Property: The Role of Zero
The identity property of addition states that adding zero to any number doesn't change its value. This means that 5 + 0 = 5, and 0 + 100 = 100. Zero is the additive identity.
4. Closure Property: Staying Within the System
The closure property indicates that the sum of two whole numbers is always another whole number. This means that the result of addition remains within the same set of numbers. This is true for other number systems as well, like integers or rational numbers.
Addition in Different Number Systems: Beyond Whole Numbers
While the examples above focus on whole numbers, addition applies to various number systems:
1. Integers: Incorporating Negative Numbers
Integers include positive numbers, negative numbers, and zero. Adding negative numbers involves moving in the opposite direction on the number line. For example, 5 + (-3) = 2. Understanding integer addition is crucial for various applications, including accounting and temperature calculations.
2. Rational Numbers: Working with Fractions and Decimals
Rational numbers encompass fractions and decimals. Adding fractions requires finding a common denominator, while adding decimals involves aligning decimal points. Understanding these processes is essential for everyday applications involving measurements and proportions.
3. Real Numbers: The Continuum of Numbers
Real numbers include all rational and irrational numbers (numbers that cannot be expressed as fractions, like π and √2). Addition with real numbers follows the same fundamental principles as with other number systems, but it extends the concept to a continuous number line.
Advanced Applications and Concepts Related to Addition: Expanding the Scope
The concept of "sum" extends beyond basic arithmetic into more complex mathematical fields:
1. Series and Sequences: Adding Infinitely Many Numbers
In mathematics, a series is the sum of the terms of a sequence. This can involve adding a finite number of terms or an infinite number of terms. Understanding series and sequences is fundamental in calculus and other advanced mathematical disciplines. Famous examples include arithmetic series (where the difference between consecutive terms is constant) and geometric series (where the ratio between consecutive terms is constant). Calculating the sum of an infinite series often involves concepts like limits and convergence.
2. Linear Algebra: Vector Addition and Matrix Addition
Linear algebra involves vector and matrix operations. Vector addition combines corresponding components of vectors, while matrix addition adds corresponding elements of matrices. These operations are crucial in computer graphics, physics, and engineering.
3. Calculus: Integration as Continuous Summation
Integration, a cornerstone of calculus, can be viewed as a continuous summation. Instead of adding discrete values, integration sums infinitely many infinitesimally small values over an interval. This finds applications in calculating areas under curves, volumes of solids, and much more.
4. Probability and Statistics: Expected Value and Summation Notation
In probability and statistics, the expected value of a random variable is calculated using summation. Summation notation (using the sigma symbol, Σ) provides a concise way to represent the sum of a series of terms. This is critical for analyzing data, making predictions, and understanding probability distributions.
Real-World Applications: The Ubiquity of Addition
The seemingly simple operation of addition is fundamental to countless real-world applications:
- Finance: Calculating total expenses, income, profits, and debts.
- Shopping: Determining the total cost of purchases.
- Measurement: Adding lengths, weights, and volumes.
- Cooking: Combining ingredients according to recipes.
- Engineering: Calculating forces, stresses, and displacements.
- Science: Analyzing data, modeling physical phenomena.
- Computer Science: Performing arithmetic operations in programming.
Conclusion: The Sum of its Parts
The answer to an addition problem is called the sum. However, this simple term belies the rich tapestry of mathematical concepts and practical applications associated with addition. From its fundamental properties to its role in advanced mathematical fields and real-world scenarios, addition remains a cornerstone of mathematics and a vital tool for understanding and interacting with the world around us. A firm grasp of addition and its implications is crucial for success in various fields and for navigating the complexities of everyday life. The seemingly simple question of "what is the answer to an addition problem called?" opens the door to a vast and fascinating world of mathematical exploration.
Latest Posts
Latest Posts
-
How Many Pages Is 5 Minutes Of Speaking
Mar 28, 2025
-
What Is The Scale Factor From Abc To Def
Mar 28, 2025
-
Words With A As The Third Letter
Mar 28, 2025
-
5 Letter Word With C In The Middle
Mar 28, 2025
-
How Tall Is An Oreo In Inches
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about The Answer To An Addition Problem Is Called The . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
