What Is 10 13 As A Percent
Arias News
May 10, 2025 · 4 min read
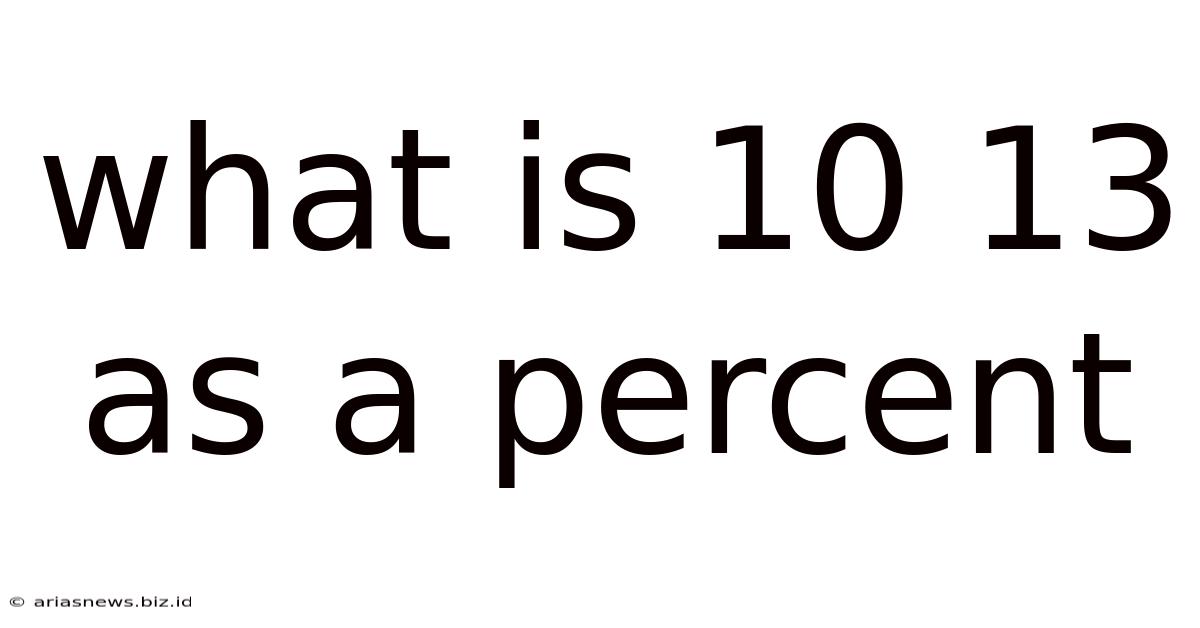
Table of Contents
What is 10/13 as a Percent? A Comprehensive Guide to Percentage Conversions
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This comprehensive guide will delve into the process of converting the fraction 10/13 into a percentage, exploring different methods and providing a deeper understanding of the underlying concepts. We'll also touch upon related concepts and offer practical examples to solidify your understanding.
Understanding Fractions, Decimals, and Percentages
Before we dive into the conversion of 10/13, let's refresh our understanding of the three key concepts: fractions, decimals, and percentages.
-
Fractions: Fractions represent parts of a whole. They are expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). In the fraction 10/13, 10 is the numerator and 13 is the denominator. This means we have 10 parts out of a total of 13 parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. Decimals are often easier to use for calculations than fractions.
-
Percentages: Percentages are a specific type of decimal representing parts of a whole expressed as a fraction of 100. The percentage symbol (%) indicates that the number is a fraction of 100. For example, 50% means 50/100, which simplifies to 1/2 or 0.5.
Method 1: Direct Conversion Using Division
The most straightforward method to convert a fraction to a percentage is through division. We divide the numerator by the denominator and then multiply the result by 100%.
Steps:
-
Divide the numerator by the denominator: 10 ÷ 13 ≈ 0.76923
-
Multiply the result by 100%: 0.76923 × 100% ≈ 76.923%
Therefore, 10/13 is approximately 76.923%.
Rounding: Depending on the level of precision required, you can round the percentage. For example, rounding to one decimal place gives us 76.9%, and rounding to the nearest whole number gives us 77%. The appropriate level of rounding depends on the context of the problem.
Method 2: Converting to a Decimal First
An alternative method involves first converting the fraction to a decimal and then multiplying by 100%.
Steps:
-
Divide the numerator by the denominator: 10 ÷ 13 ≈ 0.76923
-
Multiply the decimal by 100: 0.76923 × 100 = 76.923
-
Add the percentage symbol: 76.923%
This method yields the same result as the direct conversion method.
Understanding the Significance of Decimal Places
The number of decimal places you use will influence the accuracy of your percentage. Using more decimal places provides a more precise representation of the fraction as a percentage. However, in many practical applications, rounding to a reasonable number of decimal places is sufficient. Consider the context of your calculation; for financial applications, you might need more precision than for a simple estimation.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is invaluable in numerous real-world scenarios:
-
Calculating Discounts: If a store offers a 20% discount on an item, you can use percentage conversion to determine the actual price reduction.
-
Analyzing Financial Statements: Understanding percentages is crucial for interpreting financial data, such as profit margins, return on investment (ROI), and debt-to-equity ratios.
-
Interpreting Statistical Data: Percentages are frequently used to present statistical information, making it easier to understand and compare different data sets.
-
Calculating Taxes: Sales tax, income tax, and other taxes are typically expressed as percentages of the total amount.
-
Understanding Grades and Test Scores: Many academic assessments are expressed as percentages, reflecting the proportion of questions answered correctly.
Advanced Concepts and Further Exploration
While converting 10/13 to a percentage is a relatively straightforward process, understanding the broader mathematical concepts behind it provides a stronger foundation for more complex calculations. Further exploration could include:
-
Working with more complex fractions: Converting fractions with larger numerators and denominators or those involving mixed numbers.
-
Understanding percentage change: Calculating the percentage increase or decrease between two values.
-
Using percentages in solving equations: Integrating percentage calculations into algebraic equations.
-
Applying percentages in geometric problems: Using percentages to determine areas, volumes, and other geometric properties.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a vital skill with far-reaching applications. By understanding the different methods and practicing the calculations, you'll gain confidence and proficiency in this essential mathematical operation. Remember to consider the required level of precision and always round your answer appropriately based on the context of the problem. The ability to accurately convert fractions to percentages will enhance your problem-solving skills and empower you to confidently handle various mathematical and real-world scenarios. Mastering this skill will undoubtedly improve your numeracy and analytical capabilities.
Latest Posts
Latest Posts
-
Did Mary Ride A Donkey To Bethlehem
May 10, 2025
-
Famous People With Names That Start With Y
May 10, 2025
-
4 Out Of 11 As A Percentage
May 10, 2025
-
What Is 1 3 Of An Acre
May 10, 2025
-
What Is 8 Percent As A Decimal
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 13 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.